The ESTER project

The ambition of this project is to set out a multi-dimensional stellar evolution code, which fully takes into account the effects of rotation, tidal potential, large-scale magnetic fields, etc. in a self-consistent way. The difficult, but important point is that stars affected by large-scale effects like rotation or tidal interaction, are spheroidal and are never in hydrostatic equilibrium. They are pervaded by flows everywhere, even in the stably stratified radiative regions. These flows are essentially convective flows in thermally unstable regions (convection zones) and baroclinic flows in the radiative regions. These latter flows are grosso modo a differential rotation and a meridional circulation, with likely some small-scale turbulence. A primary motivation to include more than one dimension in models is to be able to deal with strong effects like fast rotation. Radiative regions of non-rotating stars experience very little mixing (only due to microscopic phenomena), but rotation induces flows and therefore some mixing, well-known as "rotational mixing". This is a key feature of the evolution of rotating stars. Besides, these stars also oscillate, and astronomers would like to get from the oscillation frequencies some good constraints on the structure of these stars. The foregoing reasons and many others motivated us to construct multi-dimensional models of rotating stars that will enlight us on the numerous questions we are wondering about...

The project was started Michel Rieutord. It has been strongly supported by the Programme National de Physique Stellaire (PNPS), the Action spécifique pour la Simulation Numérique en Astrophysique (ASSNA), and the CNRS in general with a two-year post-doc position in 2005-2007 given to Francisco Espinosa Lara.

The ESTER project as such was first funded by ANR in 2009-2014. The main result of this first part was the release of steady models for main sequence early-type stars (mass above 2 solar masses).

The ESTER project has been next funded under the ANR-ESRR project (Evolution Stellaire en Rotation Rapide 1/2017--1/2021), which was focusing on secular time evolution of stars and applications to the interpretation of interferometry and asteroseismology data.

The ESTER project has then been supported by the ANR-MASSIF project (2022-2025) to futher develop its applications to massive stars and their observations in interferometry.

The ESTER project is now part of the 4D-STAR project (2023-2029), funded by an ERC Synergy grant, which will make it evolve to deliver evolutionary models of stars including the three dimensions of space.

The ESTER project is also contributing to the PLATO mission by delivrering the first multi-dimensional models of solar-type stars.

1. The first ESTER Workshop: 10-11-12 June 2014 in Toulouse: see the web page for all the details of the workshop.
2. Kick-off meeting of the ANR-ESRR project: 2-3 March 2017 in Toulouse. A short summary of the meeting here. Talks have been given by:
   1. Michel Rieutord Le point sur les modeles ESTER et les challenges du projets
   2. Bertrand Putigny Les aspects 'Domain specific Language' du projet ESTER
   3. Daniel Reese Les derniers developpements du code TOP pour l'asterosismologie des étoiles en rotation rapide
   4. Damien Gagnier Initial conditions of early type stars reaching critical rotation during the main sequence"
   5. Armando Domiciano de Souza L'interprétation des données d'interférométrie stellaire
   6. Kévin Bouchaud Quelques notes sur la reconstruction du spectre continu de l'étoile theta Sco

At the moment (August 2024), the ESTER code exists in two versions: 1/ the one computing steady states of an isolated early-type star (mass larger than 2 solar masses) on the main sequence ('master' branch on github), 2/ the one computing the time evolution of a 2D-model of an isolated early-type star (mass larger than 2 solar masses) on the main sequence ('evolution' branch on github) . The only convective region computed as such is the core where isentropy is assumed. It provides the user with solutions of the partial differential equations, for the pressure, density, temperature, angular velocity and meridional velocity for the whole volume. The angular velocity (differential rotation) and meridional circulation are computed consistently with the structure as a result of the driving by the baroclinic torque.

In the evolutionary version, diffusion of hydrogen and helium are included. Please refer to Mombarg et al. (2023,2024) for more details.

Input parameters include the mass of the star, its equatorial angular velocity scaled by the critical one, the mass-fraction of hydrogen in the core. Opacity may be computed either analytically from Kramers-like formulae or from OPAL tables (Grevesse and Noels 1993 mixture), or a smoother interpolation from Houdek. Same as for the EOS which can be chosen between analytics (ideal gas+ radiation) and OPAL tables. Other parameters control the numerics.

The code uses spectral methods, both radially and horizontally, with spherical harmonics and Chebyshev polynomials. The iterations follow Newton's algorithm.

The code is object-oriented, written in C++; a python suite allows an easy visualization of the results. While running, Python graphs are displayed to show the evolution of iterations.

The code is a public code under GNU General Public License. Its first public version was hosted on the web as a Google-code and has now been moved to github at ESTER. Please refer to the Wiki pages for the installation.

Inspired by our colleagues developing the Pencil Code, we, the ESTER-project community, ask that in publications and presentations the use of the code (or parts of it) be acknowledged with reference to the web site http://userpages.irap.omp.eu/~mrieutord/ESTER.html or (equivalently) to http://ester-project.github.io/ester/. As a courtesy to people involved in the development of the program, we suggest to give appropriate reference to one or several of the following papers (listed here in temporal order):

1. Espinosa Lara F. and Rieutord M. (2007), ``The dynamics of a fully radiative rapidly rotating star enclosed within a spherical box", in Astron. Astrophys., vol. 470, p. 1013-1022

2. Rieutord M. and Espinosa Lara F. (2009), ``On the dynamics of a radiative rapidly rotating star", in Comm. Asterosismology, vol. 158., pp.~99-103

3. Rieutord M. and Espinosa Lara F. (2013), ``Ab initio modelling of steady rotating stars", in Seismology for studies of stellar rotation and convection, Edts Goupil et al., Lecture Notes in Physics, vol. 865, p. 49, Springer

4. Espinosa Lara F. and Rieutord M. (2013), ``Self-consistent 2D models of fast rotating early-type stars", in Astron. Astrophys., vol. 552, A35

5. Rieutord M., Espinosa Lara F. and Putigny B. (2016), ``An algorithm for computing the 2D structure of fast rotating stars", in J. Computational Phys.., vol. 318, 277-304 pdf

6. Zorec J., Rieutord M., Espinosa Lara F., Frémat Y., Domiciano de Souza A. and Royer F. (2017), ``Gravity darkening in stars with surface differential rotation", in Astron. Astrophys., vol. 606, A32, pdf

7. Domiciano de Souza A., Bouchaud K., Rieutord M., Espinosa Lara F. and Putigny B. (2018), ``The evolved fast rotator Sargas Stellar parameters and evolutionary status from VLTI/PIONIER and VLT/UVES", in Astron. Astrophys., vol. 619, A167 pdf

8. Gagnier D., Rieutord M., Charbonnel C., Putigny B. and Espinosa Lara F. (2019), ``Critical angular velocity and anisotropic mass loss of rotating stars with radiation-driven winds", in Astron. Astrophys., vol. 625, A88 pdf

9. Gagnier D., Rieutord M., Charbonnel C., Putigny B. and Espinosa Lara F. (2019), ``Evolution of rotation in rapidly rotating early-type stars during the main sequence with 2D models", in Astron. Astrophys., vol. 625, A89 pdf

10. Bouchaud K., Domiciano de Souza A., Rieutord M.,, Reese D. and Kervella P. (2020), ``A realistic two-dimensional model of Altair", in Astron. Astrophys., vol. 633, A78 pdf

11. Reese, D. R.; Mirouh, G. M.; Espinosa Lara, F.; Rieutord, M.; Putigny, B. (2021), ``Oscillations of 2D ESTER models. I. The adiabatic case", in Astron. Astrophys., vol. 645, A46 pdf

12. Lazzarotto A., Hui Bon Hoa A. and Rieutord M. (2023) ``Photometric determination of rotation axis inclination, rotation rate, and mass of rapidly rotating intermediate-mass stars", in Astron. Astrophys., vol. 676, A50 pdf

13. Mombarg J., Rieutord M. and Espinosa Lara F. (2023) ``The first two-dimensional stellar structure and evolution models of rotating stars. Calibration to β Cephei pulsator HD192575", in Astron. Astrophys., vol. 677, L5 pdf

14. Mombarg J. S. G., Rieutord M. and Espinosa Lara F. (2024), `` A two-dimensional perspective of the rotational evolution of rapidly rotating intermediate-mass stars. Implications for the formation of single Be stars", in Astron. Astrophys., vol. 683, A94 pdf

Some Results

The history of modelling rotating stars in two-dimensions can be found here: Modeling rapidly rotating stars in Proceedings of SF2A Annual meeting , p. 501-506

A first investigation of the baroclinic flows in stars: Rieutord M. (2006), The dynamics of the radiative envelope of rapidly rotating stars. I. A spherical Boussinesq model, ref. Astron. Astrophys., vol. 451, p. 1025-1036

A first "realistic" model of a completely radiative star encapsulated in bounding sphere may be found in Espinosa Lara F. and Rieutord M. (2007), The dynamics of a fully radiative rapidly rotating star enclosed within a spherical box, ref. Astron. Astrophys., vol. 470, p. 1013-1022

The same but now with a spheroidal boundary which spouses an isobar surface; in Rieutord and Espinosa Lara (2009), On the dynamics of a radiative rapidly rotating star, in Comm. Asterosismology, vol. 158., pp.~99-103

We show here how the gravity darkening (i.e. the latitude variation of the surface brightness) can be modelled by a single parameter (the ratio ω of actual rotation to the critical one) instead of two in previous models (ω and β an exponent, controlling the relation between effective temperature and effective gravity); see Espinosa Lara and Rieutord (2011), Gravity darkening in rotating stars. The foregoing approach is called the omega-model or ω-model, and has been detailed in the proceedings Rieutord (2016) Physical processes leading to surface inhomogeneities: the case of rotation in Lecture Notes in Physics, vol. 914, p. 101-125

The preceding results have been extended to binary stars and it was shown in passing that the old result of Lucy (1967) that gravity darkening exponent in low-mass stars is β=0.08, cannot be used to model actual gravity darkening on stars with variable surface gravity. This exponent is only valid for spherically symmetric models and comes from the surface opacity law. See Espinosa Lara and Rieutord (2012), Gravity darkening in binary stars.

A synthesis of the results dating October 2011 may be visualized in this pdf presentation given by F. Espinosa Lara at Santa Barbara conference on Asteroseismology KITP Conference

A first detailed account on the ESTER code: the physics of the model, its mathematical description, its numerical technique and the first results. These models give the characteristics of stars with mass in the range 2 to 20 solar masses, rotating up to 98% of the break-up velocities. These models describe steady-state solutions of the 2D stellar structure solution including for the first time a self-consistent determination of the differential rotation and the associated meridian circulations; see Rieutord and Espinosa Lara (2012), Ab initio modelling of steady rotating star in Seismology for studies of stellar rotation and convection, Edts Goupil et al., Lecture Notes in Physics, vol. 835, p. 49, Springer. and Espinosa Lara and Rieutord (2013), Self-consistent 2D-models of fast rotating early-type stars, in Astron. Astrophys., vol. 552, A35

A detailed presentation of the ESTER code, with its numerical performance (spectral convergence for instance) may be found in Rieutord et al. (2016) An algorithm for computing the 2D structure of fast rotating stars, in J. Computational Phys.., vol. 318, 277-304.

ESTER has been used to model the evolution of the rotation of massive stars. Such stars indeed lose mass and therefore angular momentum since they rotate. This investigation was realized by Damien Gagnier during his PhD thesis and is detailed in 2 papers Gagnier et al. (2019a) Critical angular velocity and anisotropic mass loss of rotating stars with radiation-driven winds and Gagnier et al. (2019b) Evolution of rotation in rapidly rotating early-type stars during the main sequence with 2D models (see Astron. Astrophys., vol. 625, A88, A89).

The following application of ESTER has been devoted to derive a concordance model of Altair, a nearby fast rotating A-type star. The challenge that was taken up by Kévin Bouchaud during his PhD thesis was to devise a model that matches all the known observational constraints of Altair. These constraints are interferometric observations (from ESO PIONIER and GRAVITY interferometers), spectroscopic and asteroseismic observations. The main results of this study may be summarize in the mass and age derived for Altair, namely 1.86Msun and 100Myrs, so barely off the ZAMS. Details in Bouchaud et al. (2020) A realistic two-dimensional model of Altair. An improved age of Altair, based on asteroseismic data from the TESS satellite, has been determined by Rieutord et al. (2024)

ESTER models have now been coupled to PHOENIX models of atmosphere in order to derive spectroscopic quantities and invert them. This has been the work of Axel Lazzarotto for his PhD Thesis. The results of this work may be found in Lazzarotto et al. 2023

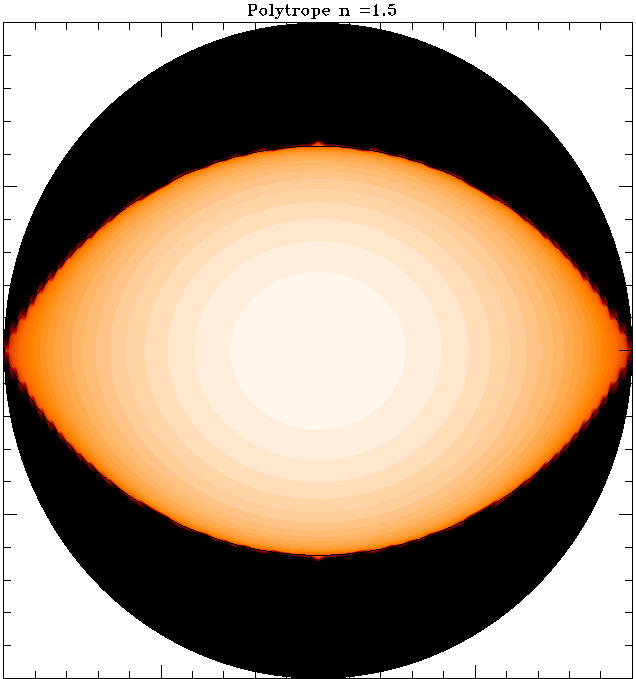
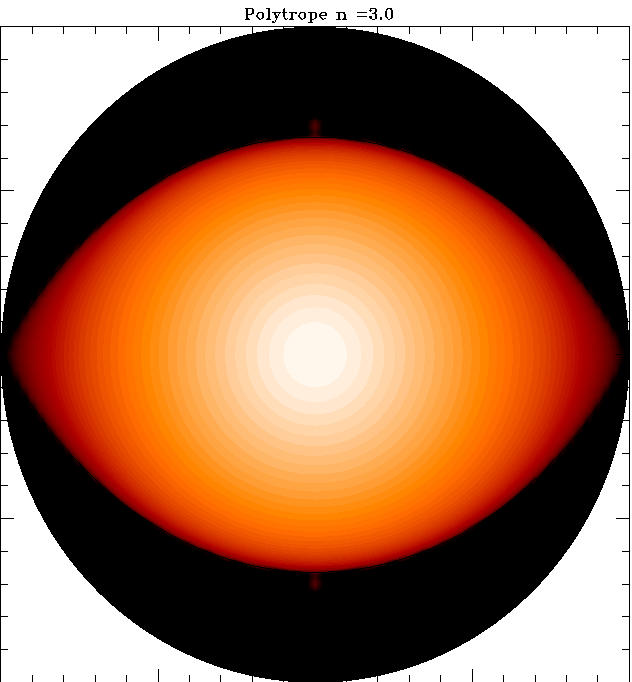
A representation of the discretization grid: the star is shaded and split into several layers; the outer white region is an outer vacuum domain where only the gravitational potential is computed.	The shape of a n=3/2 polytrope rotating close to the break-up velocity.	The same for a n=3 polytrope; note that as this polytrope is more centrally condensed, its inner regions are less flattened.

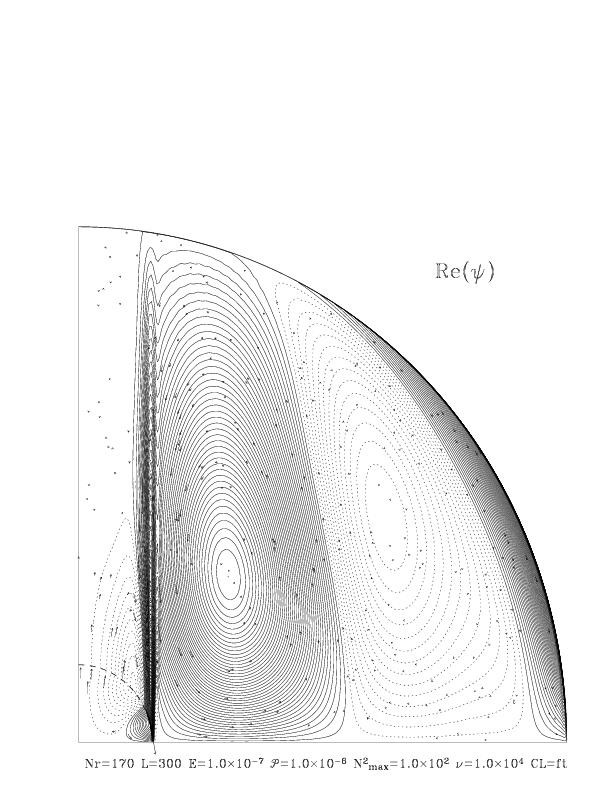
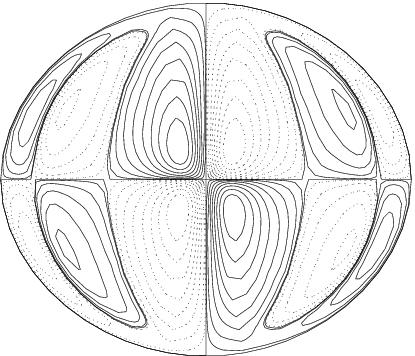
On the top row we see the meridional circulation and differential rotation as predicted by a simplified Boussinesq model of a massive star (see Rieutord 2006 for details). In the bottom row we show the computed differential rotation of a purely radiative star, with realistic physics (see Espinosa Lara and Rieutord 2007).

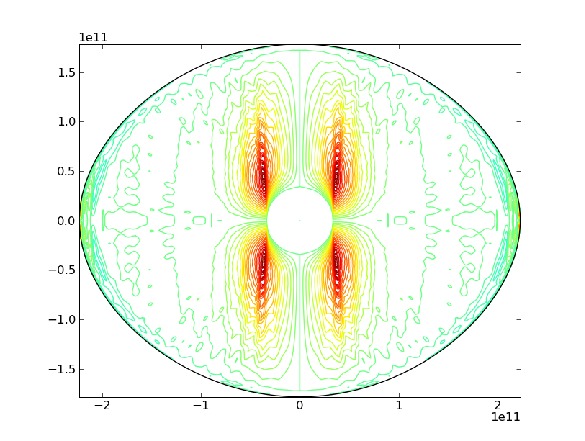
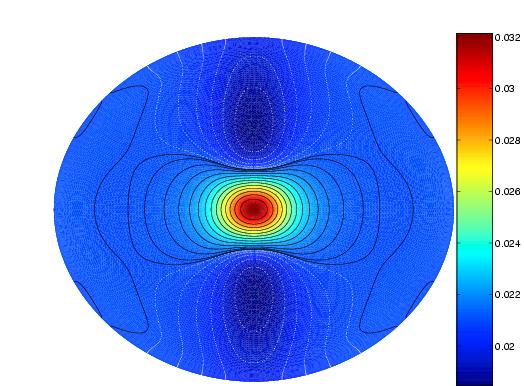
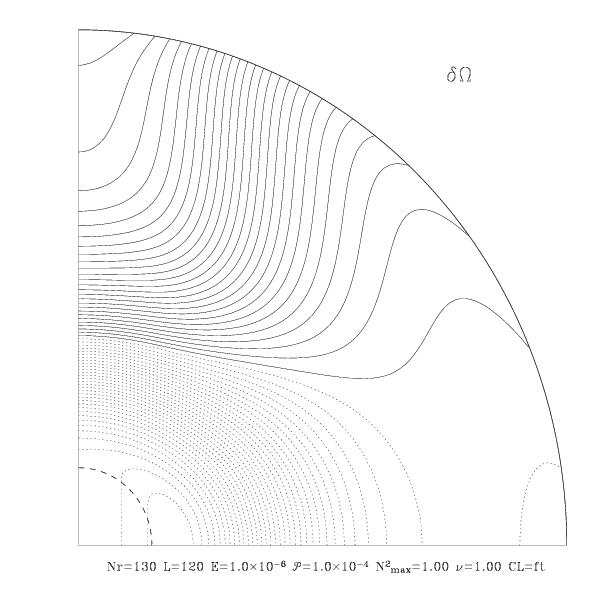
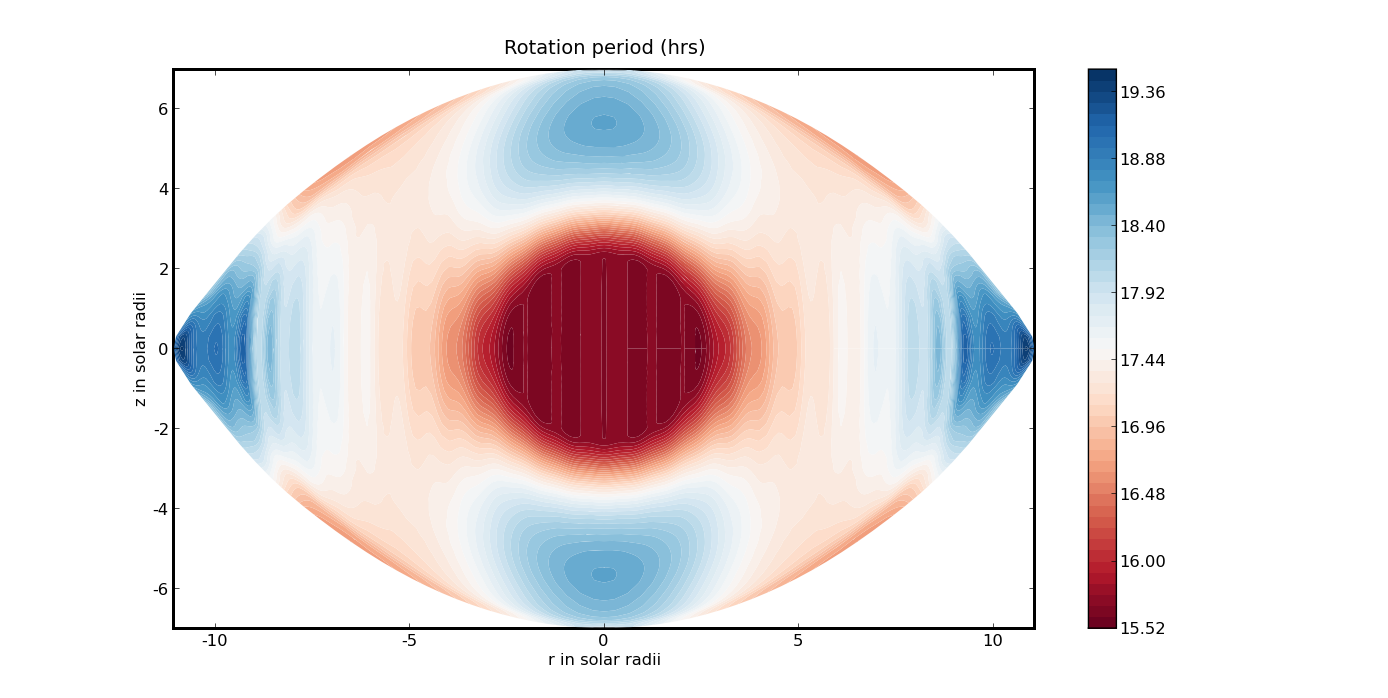
Left: Differential rotation in a 5 solar mass star rotating at 70% of the critical angular velocity. Abundances are solar. Note the similarity with the fully radiative star. Inside the convective the rotation is cylindrical (more details in Rieutord and Espinosa Lara 2012). Right: The associated meridian circulations. The cells attached to the convective core are the trace of the Stewartson layers when no viscosity is present in the bulk of the fluid and at finite numerical resolution. Spatial resolution: 400 Chebyshev polynomials+64 spherical harmonics.

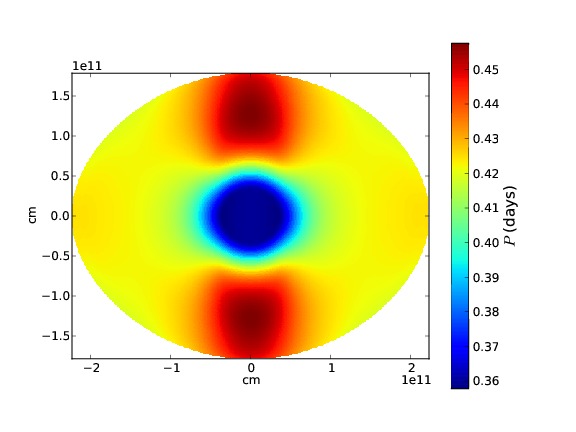
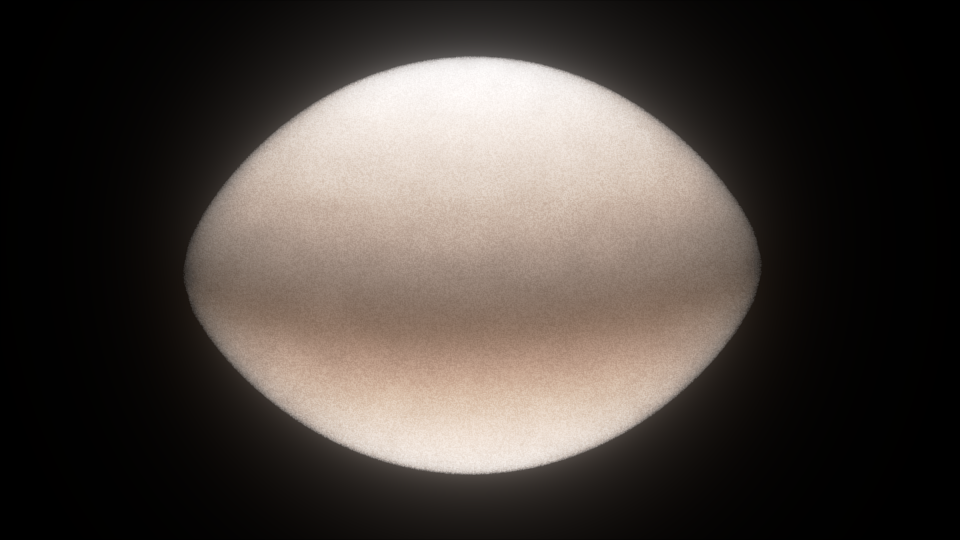
Left: Gravity darkening for an intermediate mass star rotating at 90% of the critical angular velocity. Abundances are solar. Right: The differential rotation of a 30 solar mass ZAMS star rotating at 98% of the critical angular velocity. The ratio of equatorial radius to polar radius is 1.56.

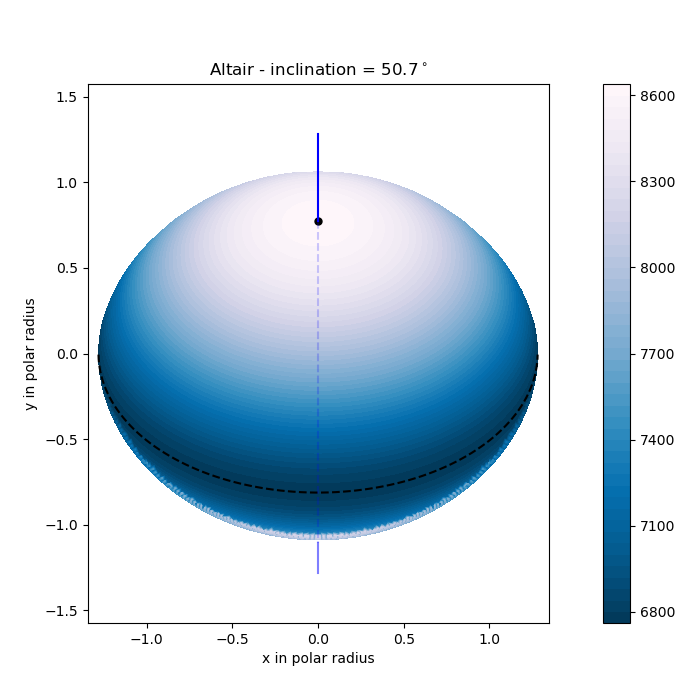
Left: The Be star (around 6 solar mass) Achernar modelled by ESTER as it is viewed in the sky. Right: The flux at the surface of Altair as given by the concordance model of Bouchaud et al. (2020).

More to come soon ...

---

---