Rotating Fluids: the theory
In astrophysical and geophysical fluids rotation is often playing an
important
part. In these common cases, the Coriolis force is the dominant force.
Fluid motions under this force show a tendancy of being invariant
with respect to the coordinate along the axis of rotation. This is a
consequence of the so-called Taylor-Proudman theorem which applies to
quasi-steady flows.
When the flows are not steady, but the Coriolis force
is still dominating all other effects (nonlinearities or viscosity), then
we are facing wave motions, namely inertial waves, for which the Coriolis
force is the restoring force. Such waves have very strange properties:
the phase and the energy propagate in perpendicular directions! In
addition, when the fluid is contained in some finite volume, the mode of
oscillation of the fluid obey the Poincaré equation which is a hyperbolic
equation. This is strange because the Poincaré equation governs
the pressure perturbations which meet boundary conditions. A hyperbolic
equation plus boundary conditions make an ill-posed boundary value problem as
mathematicians say. However, such ill-posed problems are quite difficult
and, for instance, the solutions of the Poincaré equation, when
the fluid is in a spherical shell, have been uncovered only recently
(Rieutord and Valdettaro 1997, Rieutord et al. 2001), while they have
been known for more than a century for the full sphere (Bryan 1888).
The difficulty of this problem comes from its 'ill-posedness' and
the non-separability of the variables for containers like the spherical shell:
this yields many singularities; in fact all solutions but a few ones are
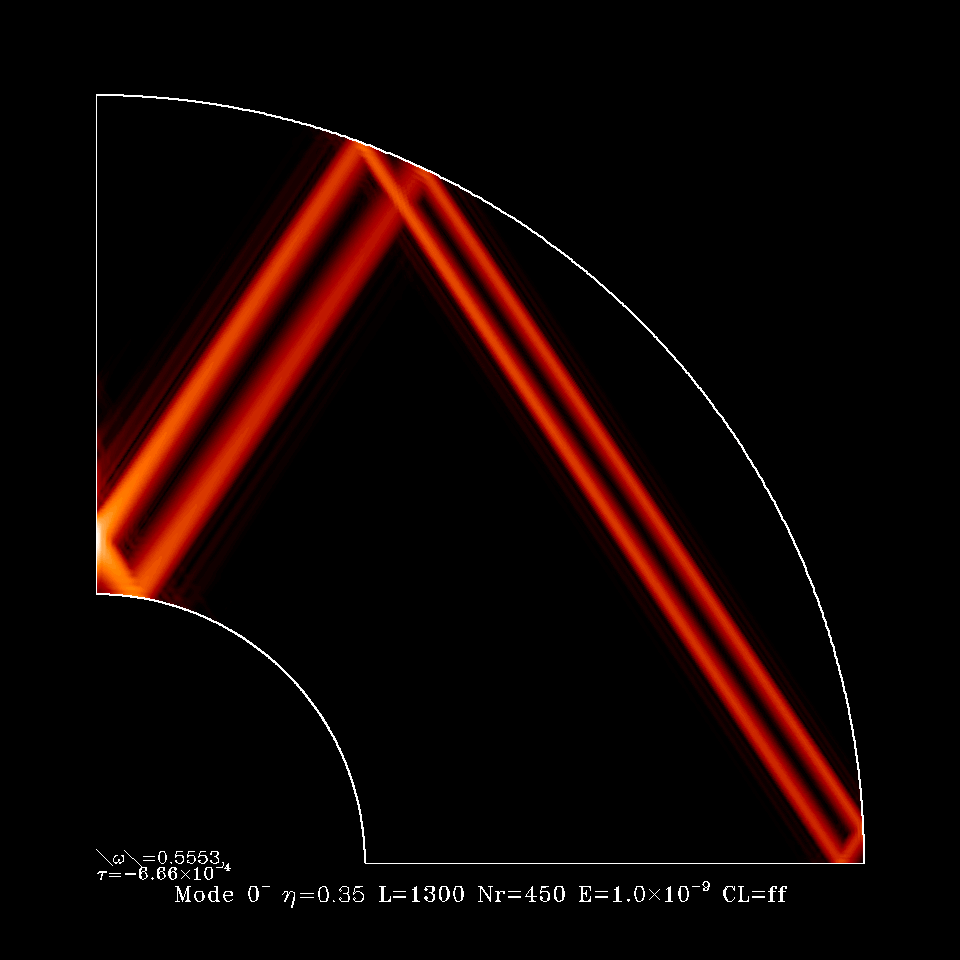
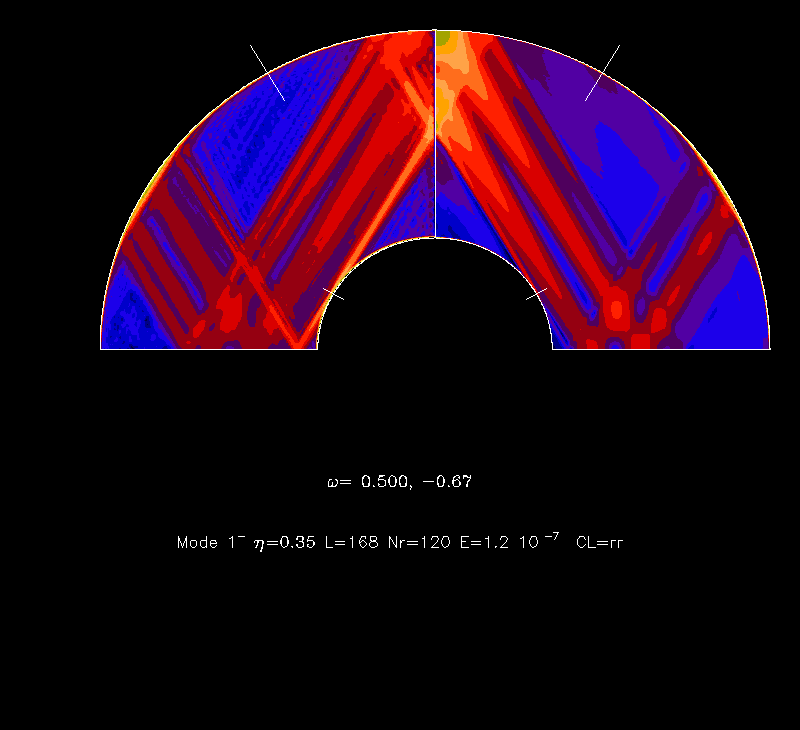
singular. These singularities generate shear layers when the viscosity
of the fluid is taken into account. These singularities are the 'rays' which
show up in a meridional plane of a spherical shell when the kinetic energy
density is plotted. This is what is shown on the figures below

Some good reading :
-
Rieutord M. (1987),
Linear theory of rotating fluids using spherical harmonics
- I. Steady flows. Geophysical and Astrophysical Fluid Dynamics, vol.
39, p. 163--182.
-
Rieutord M. (1991), Linear
theory of rotating fluids using spherical harmonics - II. Time-Periodic
flows. Geophysical and Astrophysical Fluid Dynamics vol. 59,
p. 185--208.
-
Rieutord M. and Valdettaro L. (1997),
Inertial waves in a rotating spherical
shell, J. Fluid Mech. vol. 341, p. 77--99.
-
Dintrans B., Rieutord M. and Valdettaro L. (1999), Gravito-inertial
waves in a rotating stratified spherical shell, J. Fluid
Mech. vol. 398, p. 271--297,
-
Rieutord M. and Noui K. (1999),
On the analogy between gravity modes and inertial modes in spherical
geometry, European Physical Journal B vol. 9, p. 731-738.
-
Rieutord M., Georgeot B. and Valdettaro L. (2000), Wave
attractors in rotating fluids: a paradigm for ill-posed Cauchy
problems, Phys. Rev. Letters , vol. 85, pp. 4277--4280
-
Rieutord M., Georgeot B. and Valdettaro L. (2001), Inertial
waves in a rotating spherical shell: attractors and asymptotic
spectrum, J. Fluid Mech., vol. 435, p. 103--144
-
Rieutord M., Valdettaro L. and Georgeot B. (2002), Analysis
of singular inertial modes in a spherical shell: the slender toroidal
shell model, J. Fluid Mech., vol. 463, p. 345-360
- Rieutord M. and Valdettaro L. (2010),
Viscous dissipation by tidally forced inertial modes in a
rotating spherical shell, in J. Fluid Mech., vol. 643,
p. 363-394
- Baruteau C. and Rieutord M. (2013),
Inertial waves in a differentially rotating spherical shell
, in J. Fluid Mech., vol. 719, p. 47-81
- Rieutord M. and Valdettaro L. (2018),
``Axisymmetric inertial modes in a spherical shell at low Ekman numbers
, in J. Fluid Mech., vol. 844, p. 597-634


