FOCUSING TELESCOPES IN NUCLEAR ASTROPHYSICS

FOCUSING PRIMER

Since the wavelength of nuclear gamma-ray photons is two to three orders of magnitude shorter than the distance between atoms in solids, astrophysicists have been used to accept that it is ãimpossible to reflect or refract gamma-raysä. Consequently, present types of telescopes for nuclear astrophysics are based on inelastic interaction processes : most of the instruments are based on geometrical optics (coded aperture instruments) or quantum optics (Compton Telescopes). 

Because the collecting area of such systems is equal to the detector area, nuclear astrophysics has come to a mass-sensitivity impasse where ãbigger is not necessarily betterä. Improving the sensitivity of an instrument can usually be obtained by a larger collection area - in the case of classical gamma-ray telescopes this can only be achieved by a larger detector surface. Yet, since the background noise is roughly proportional to the volume of a detector, a larger photon collection area is synonymous with higher instrumental background. For such ãclassicä gamma-ray telescopes, the sensitivity is thus increasing at best as the square root of the detector surface. 

The ensuing mass/sensitivity dilemma can ultimately only be overcome by concentrating gamma-rays, taking advantage of the phase information of the gamma-ray photons : A gamma ray optical system is designed to concentrate radiation - by surface reflection, diffraction and/or refraction - collected from a large area into a small focal spot. This allows a modest size, well shielded detector to register a much larger signal than it would have intercepted if it was exposed to the radiation field directly. 

Table 1 : Focusing Systems for High-Energy Photons

Wolter telescopes	a) total external reflection b) multilayer mirror interference	~ 0.1- 12 keV ~ 20 - 100 keV
Lobster eye telescopes	total external reflection	0.1-3.0 (+) keV
Capillary Concentrators	total external reflection	1 - 60 keV
Kirkpatrick/Baez Optics	total external reflection
Bragg-Lenses	Bragg (surface) diffraction	10 - 200 keV
Laue-Lenses	Laue (volume) diffraction	200 keV- 2 MeV
Fresnel lenses	refraction / diffraction	1 keV - 10 MeV

Table 1 lists the concepts, main instrumental features, and energy range of various focusing systems for high-energy photons. While grazing incidence focusing based on total external reflection is widely used in X-ray astronomy, gamma-ray astronomy suffers from the lack of focusing. This workshop therefore focuses on the concentration of gamma-rays - this is : diffraction in Fresnel, Bragg- and Laue-Lenses and other innovative techniques.

Multilayer mirrors

In order to cover energies up to ~100 keV - and maybe even beyond - the above mentioned geometries for grazing incidence telescopes can be used with multilayer coatings as mirror surface. (At present, the highest energy focused by total external reflection is 45 keV, and has been achieved during a balloon flight of the HERO payload in 2001 using iridium-coated mirrors). Presently a number of Multilayer Mirrors are under development for use in Wolter telescopes. Although the reflectivity of a single mirror surface at incidence angles greater than the critical angle q_c  is very small, it is not zero, hence a small fraction of the radiation is reflected at reasonably large incidence angles.
 Multilayers coatings consist of alternating layers of high and low index n of refraction materials : The reflection by a multilayer mirror is described by the constructive interference of the reflections at all low-high n interfaces This result in a sizable total reflectivity of the system. Similar to the Bragg-diffraction in crystals (see next section), the reflections have to be added with the correct phase relationship, leading to a boundary condition that relates incidence angle q_l, layer thickness d_l and wavelength l
 

2 d_l sin q_l      =     n l

where n, the order of the reflection is an integer >= 1(multilayers are most commonly used in the first order, n = 1). Consequently, the response of so called Uniform Period Multilayers results in a narrow energy-bandpass. High reflectivity in a broad energy-bandpass can be achieved with graded  multilayer coatings, here the film thickness d is varied over the stack. These Extremely Broad Band (EBB) Multilayers with reflectivities over bandpasses of > 20 keV are being intensely developed by several groups (HEFT, InFOCuS). The materials for the reflector/spacer coatings are selected for their different indices of refraction and for minimum absorption - presently considered material combinations are W/Si, W/C, Ni/C, and Pt/C. A first balloon flight using a  20-40 keV bandwidth mirror utilized at about ~0.2° incidence angle has been performed  by the InFOCuS project in 2001. Development work for the hard X-ray telescope on the Constellation-X satellite has indicated potential up to around 200 keV for this technique.

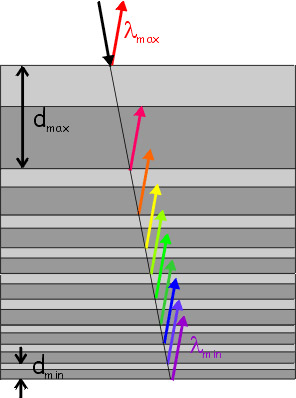
Figure 1 : The bilayer thickness varies continuously with depth in a graded multilayer film. Each bilayer effectively reflects a different X-ray wavelength, so by adjusting the distribution of bilayer thicknesses broadband reflectance can be achieved.

Crystal Diffraction Lenses

Diffraction lenses use the interference between the periodic nature of light and a  periodic structure such as the matter in a crystal. An elementary derivation of the Bragg condition,  2 d_B sin q_B = n l; it is assumed that the incident waves are reflected by the parallel planes of the atoms in the crystal. (q_B is the Bragg angle, n is an integer denoting the diffraction order, l is the wavelength of the gamma-ray being diffracted, and d is the spacing between the crystalline planes used in the diffraction process). There is constructive interference if the optical path difference between neighboring paths is a multiple of the wavelength nl. 

Bragg- vs. Laue geometry : The Bragg condition implies that higher incoming photon energies require smaller Bragg angles. At gamma-ray energies, Bragg angles are generally less than one degree. The reflection can be at the surface (so-called Bragg geometry) or the beam can pass through the crystal volume (so-called Laue geometry). The maximum efficiency for diffraction in the Bragg geometry is close to 100% (assuming no absorption). 

A hard-X ray lenses operating in Bragg geometry using mosaic pyrolithic graphite crystals has been proposed by Frontera et al 1995.The concentrator consists of 28 confocal parabolic mirrors. Each mirror is made up of small pieces of mosaic crystal with the diffraction planes parallel to the parabolic surface, which results in a broadband energy response. The outer diameter is 1.3 m, the focal length is 3.8 m. The effective area is 1000 cm2 at 15 keV decreasing to 35 cm2 at 100 keV. An angular resolution of a few arc minutes could be achieved. 

For higher energies, Laue geometry is a more appropriate choice : due to the small Bragg angles at high energies, the crystal area in Bragg geometry becomes extremely long. At such energies, the crystal areas needed for Bragg type diffraction would be 100 times the area of crystals used with Laue diffraction : for a 1-cm beam and a Bragg angle of 1 degree, the crystal length L = A/sinq_B would be 57 cm! Laue geometry ãonlyä allows maximum efficiencies of < 50 % (assuming no absorption in the crystal). However, the attenuation due to the beam passing through the crystal becomes small at high energies, making Laue geometry possible. In the following, gamma-ray lenses using Laue geometry are discussed. 
 

Laue geometry lenses : In a crystal diffraction lens, crystals are usually disposed on concentric rings such that they will diffract the incident radiation of a same energy onto a common focal spot (Fig 2). A crystal at a distance r1 from the optical axis is oriented so that the angle between the incident beam and the crystalline planes is the Bragg angle q B1. Its rotation of around the optical axis results in concentric rings of crystals. With  the same crystalline plane [hkl] used over the entire ring, the diffracted narrow energy band is centered on E1.

Two subclasses of crystal diffraction lenses can now be identified - narrow bandpass Laue lenses and broad bandpass Laue lenses. 

Narrow bandpass Laue lenses use a different crystalline plane [hkl] for every ring in order to diffract photons in only one energy band centered on an energy E1=E2. 

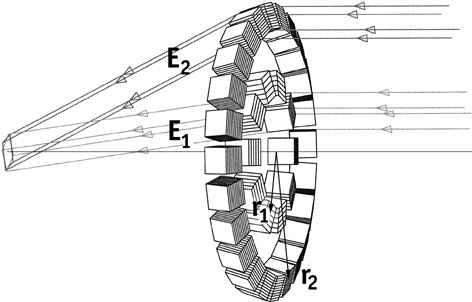
Figure 2 : The basic design of a crystal diffraction lens in Laue geometry: 

As the diffraction efficiency decreases with increasing diffraction order n, a crystal in an exterior rings will add less efficient area to the lens than a crystal on an inner ring. However, since the number of crystals increases with the ring-radius, all rings will usually contribute about the same amount of efficient area to the lens. Using larger and larger Bragg angles with increasing ring radius allows the instrument to be relatively ãcompactä, featuring a shorter focal length than a broad bandpass Laue lens with an equivalent amount of efficient area for energy E1. This type of instrument has been developed for use in nuclear astrophysics by the CLAIRE collaboration. An example of a narrow bandpass Laue lens, the balloon telescope CLAIRE, which was succesfully flown in 2001.

Fresnel lenses

Fresnel lenses can focus gamma-rays by using a combination of diffraction and refraction. Because the wavelengths of gamma-ray are so short and the penetrating power high, a phase shift can be achieved in a thickness of material which has a high transparency.

This type of gamma-ray lens has been proposed by Skinner in 2001 - Fresnel lenses have the potential for revolutionizing gamma-ray astronomy : a telescope based on these principles can have angular resolution better than a micro second of arc - sufficient to resolve the event horizon of black holes in the nuclei of AGNs. At the same time, the sensitivity can be three orders of magnitude better than that of current instrumentation.
Diffraction-limited lenses of several meters in size are feasible and do not require high technology for their manufacture. Focal lengths are long ? up to a million kilometers ? but developments in formation flying of spacecraft make possible a mission in which the lens and detector are on two separate spacecraft separated by this distance. 

Fresnel zone plates : In a Fresnel zone plate (Figure 3) radiation is brought to a focus by blocking parts of the wave front which would arrive at the focal point with an incorrect phase. One can considers a part of the zone plate towards the periphery as a diffraction grating which deviates the radiation towards the focal point. It can then readily be seen that the efficiency for concentrating the radiation into the first order (k=1 ) focal point cannot exceed pi² , i.e.about 10%, because energy also goes into the zero order (k=0; straight through) and into orders with k>1 and k<0. The energy in these orders is in proportion to the power in the corresponding components in the Fourier transform of a square wave with transmission between zero and one. 

Phase Fresnel Lenses : By varying the optical thickness, and hence the phase of the transmitted radiation rather than its amplitude, across the zone plate (Fig 3), all of the power can be diffracted into the principle (k=1 ) focus in a configuration we shall refer to here as a ãPhase Fresnel Lens ä. The phase shift necessary is, of course, never greater than 2 pi. 

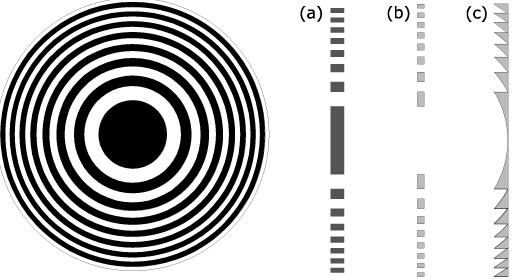
Fig.3 a) Fresnel Zone Plate with absorbing and transmitting zones b) Phase Zone Plate c) Phase Fresnel Lens
 

The focal length of the lens is a function of the zone widths, characterized by the value pmin at the outer rim where they are finest : 
 

 f      =   (d p_min / 2l )    =     0.4*10⁶ (d/1m)(p_min/1mm)(E/1MeV) km 

Thus very large lens-detector separations are implied. However, with the development of formation flying for space based interferrometry, separations of the order of 10⁶ km are no more looking ridiculous. Such distances have the benefit of offering a ãplate scaleä which is convenient for ultra-high angular resolution observations.

Update : September 2005
Questions and comments : Peter von Ballmoos