Enseignant : Laurent Koechlin

Ce cours fait suite au cours de physique stellaire et planétaire fait par Peter von Ballmoos
 
 

Table des matières :

            Dans la page précédente

Unités, Notations, Constantes, alphabet

1.  Echelles et distances cosmologiques

2. Techniques de mesure

3. Instrumentation

4.  Galaxies
 

            Dans cette page

5. Structure à grande échelle

6. Isotrope ou Anisotrope?

7. Gravitation et courbure
 

        Corrigé des exos (en format pdf)

Sites web à explorer :

IMAGES HUBBLE
IMAGES HDF sud

5.1 Amas de galaxies

Les galaxies se regroupant en amas, par exemple l’amas local contenant notre galaxie et une quinzaine d’autres dont M31. On a de nouveau le problème de la masse manquante quand on compare la masse d’un amas de galaxies à la somme des masses des galaxies visibles dans l’amas :

Objet rapport Masse / Luminosité
Amas de galaxies : 100 à 200.

La distance moyenne entre galaxies dans un amas est de l’ordre de 20 fois leur diamètre ; la probabilité qu’une collision ou une rencontre proche ait lieu n’est pas négligeable. On observe en effet une douzaine galaxies en interaction gravitationnelle proche parmi les 4000 du catalogue NGC.

Lors d’une collision entre deux galaxies, les gaz subissent une forte compression et un fort taux de formation stellaire. Ils disparaissent dans ce processus. On observe une émission X provenant de gaz diffus très chauds dans les amas. Ces gaz peuvent provenir de galaxies entrées en collision. Les étoiles des deux galaxies se mélangent. L’énergie cinétique ne peut pas être dissipée microscopiquement comme dans un choc inélastique. Elle se retrouve sous forme d’énergie orbitale des étoiles : la structure en disque disparaît pour laisser place à des orbites aléatoires (augmentation de l’entropie) et au bout de 10 8 ans environ la nouvelle galaxie formée des deux précédentes prend une forme elliptique. La durée du processus de collision est évaluée à 3 10 8 ans par des modèles numériques.

Sur l’ensemble du catalogue NGC,  0.3 % des galaxies sont en collision. Si la probabilité de collision est restée constante depuis la naissance de l’univers il y a 15 10 9 ans, environ 15 % des galaxies doivent avoir subi des collisions. La proportion observée de galaxies elliptiques est de 20 à 30 %. On pourrait expliquer leur origine par la collision de galaxies spirales.

Le regroupement en amas de fait à plusieurs échelles :

15 galaxies dans un rayon de 0.7 Mpc (amas local)
10 4 galaxies dans un rayon de 3 Mpc (amas denses)
100 amas dans un rayon de 30 Mpc.

Exemple d’amas :      nb. de galaxies      distance
 Virgo                           10 ³                     16 Mpc
 Coma                            10 ⁴                  100 Mpc

Les amas de galaxies sont les structures les plus grandes qui peuvent être liées par la gravitation. Pour des volumes plus grands, l’expansion fait que les vitesses au bords sont supérieures à la vitesse de libération.

5.2 Sursauts Gamma

L’bservation des Gamma d’origine cosmique nécessite de soritr de l’atmosphère, qui les absorbe. Les premiers satellites gamma ont observé des sources continues (résidus de supernovas, galaxies actives) et des émission très intenses mais de très courte durée, et jamais au même endroit. Ce sont les sursauts Gamma.

1)  Soit deux étoiles à neutrons identiques de 1 masse solaire chacune en orbite circulaire. donner l’expression de la vitesse orbitale en fonction du rayon de l’orbite.

2) L’orbite a un rayon r1 = 10 km. Quelle est la vitesse orbitale ? Quelle est la période orbitale ?

3) Quelle est l’énergie potentielle gravitationelle du système, son énergie cinétique et son énergie totale ?

4) On considère que les pertes d’énergies par rayonnement d’ondes gravitationelles vont faire tomber les deux étoiles l’une sur l’autre. Cela va former un trou noir de deux masses solaires. Quel est le rayon de Schwarzschild de ce trou noir ?

5) Pour avoir un ordre de grandeur de l’énergie dégagée par la formation de ce trou noir, on va calculer la différence d’énergie mécanique entre celle du système dans sa situation initiale (r=10 km) et celle ou les deux centres de masse seraient séparés par le rayon de Schwarzschild du trou noir en formation. Donnez la formule, et la valeur de cette énergie.

6) Si l’on considère cet énergie comme rayonnée de manière quasi instantanée par une zone explosive de 3 x 108 m de rayon, quelle est la durée observée du phénomène depuis la terre ? Quelle est la puissance rayonnée ? Comparer à celle du soleil et à celle d’une galaxie.

7) On considère que 70% de cette énergie est rayonnée sous forme de gammas de 100 keV en moyenne. On détecte 1000 gammas en une seconde à l’occasion d’un sursaut avec un détecteur de 40 cm2.    Quel est l’éclairement reçu en Wm-2 ?

8) En considérant que le rayonnement de la source du sursaut est isotrope, qu’il n’y a pas d'absorption sur le trajet, donner la distance de la source du sursaut. Au vu du résultat, Aurait-il fallu prendre en compte l’effet du Z ?

5.3 Bulles cosmiques

L’univers est-il isotrope à très grande échelle ? En traçant un diagramme 3D des galaxies et amas observés jusqu’à 600 Mpc il semble que ce n’est pas le cas : on trouve une répartition des amas le long de filaments et sur la surface de “bulles” à l’échelle de la centaine de Mpc. Une structure très marquée visible sur plus de 180 ° a été baptisée “Le grand mur”. L’isotropie réapparaît à plus grande échelle encore mais on dispose de peu d’observations directes. A l’échelle du Gpc on pourrait considérer l’univers comme une sorte de mousse dont les parois des bulles seraient formées d’amas de galaxies, et le creux de bulles des immenses zones vides.
 
 

6.1 Expansion isotrope.

Depuis la terre, on observe que les galaxies et amas lointains s’éloignent de nous à une vitesse proportionnelle à leur distance (loi de Hubble)

d = v / H_o avec H_o - 70 ± 25 km s^-1 Mpc^-1

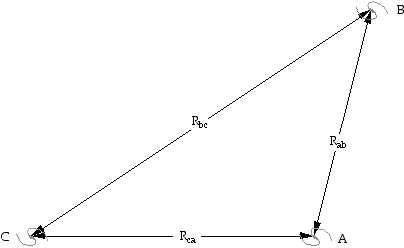
Cette propriété est-elle spécifique à notre position dans l’univers ? Il est facile de démontrer le contraire. Prenons trois galaxies A, B et C et des observateurs sur chacune.

Si nous sommes en A nous observons :

  V_ab = H_o R_ab  et V_ac = H_o R_ac

V et R sont des vecteurs, on a donc :

  R_bc = R_ac - R_ab  et V_bc = V_ac - V_ab

=>     V_bc = H_o R_bc

L’observateur sur la galaxie B verra exactement la même loi d’expansion que  nous (quelle soit la direction pointée).  Ceci est valable quel que soit B, donc l’expansion observée depuis la terre reste la même quel que soit le point de l’univers d’où on l’observe. Elle n’est pas spécifique à un point donné mais isotrope.
.

Si l’on appliquait la loi de Hubble :     v = H_o d      sans limite de distance, Pour quelle distance arriverait-on à la vitesse de la lumière ?
On rappelle : Ho = 70 km s ^-1 Mpc ^-1
Que vaudrait le décalage spectral z d’un objet à cette distance ?
A quoi correspondrait cette distance ?
.

La gravitation agit à long terme sur l’expansion. Dans un univers infini et isotrope à grande échelle on suppose que la densité est uniforme (à partir d’une certaine échelle). Prenons une sphère de rayon r et de densité r_mo , sa masse s’exprime :
 M = r_mo 4p  r³ / 3                                                                         (6.2-1)

Toutes les galaxies à l’intérieur de cette sphère suivent le mouvement d’expansion.  la masse totale M contenue dans la sphère ne change pas avec l’expansion mais son rayon croît. L’énergie totale d’une galaxie de masse m à la surface de cette sphère sera la somme des énergies cinétiques et potentielles :

 E  = 1/2 mv² - GMm r ^-1                                                                (6.2-2)

Si la vitesse v de la galaxie par rapport au centre de la sphère est due à l’ expansion de l’univers :

  v = H_o r  =>
 E = (1/2) m H_o² r² - G rm_o (4/3)  p  r ³ m r^-1                               (6.2-3)
 E = r² m  [ (1/2)  H_o² - (4/3) p G r_mo ]                                        (6.2-4)

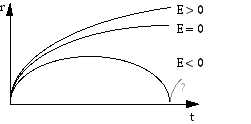
Une énergie totale positive correspond à une vitesse de la galaxie supérieure à la vitesse de libération, elle n’est pas liée gravitationnellement à la masse M et l’expansion continuera indéfiniment. Une énergie négative limitera l’expansion à un rayon maximum, puis la transformera en contraction. On peut aussi mettre l’équation (6.2-4) sous la forme :

 6 E/ (r ² m) =  3 H_o² - 8 p G r_mo                                               (6.2-5)

L’inéquation E > 0 donnera une contrainte sur la densité r_mo :
 E > 0    =>   r_mo < 3 H_o² / 8p G

exercice 6.2 : Densité de l’univers

Comparer la densité moyenne observée localement avec 3 Ho2 / 8? G , valeur limite donnant E = 0.
Pour l’amas local la masse totale des étoiles et nuages de gaz détectés optiquement correspond à 6 10 11 masses solaires. Pour simplifier on prend comme volume celui d’un cube de 5 Mpc de côté.
H_o = 70 km s^-1 Mpc^-1
G = 6.67 10^-11
Masse solaire = 1,989 * 10 ³⁰ kg

Comme la vitesse de récession des galaxies est modifiée dans le temps par la gravitation, la loi de Hubble s’écrit :

 v(t) = H(t) r(t)

On appelle H_o la valeur présente de H(t). Par convention, on donne l’indice o aux valeurs correspondant au présent : r_o pour la densité actuelle de l’univers, t_o pour l’âge de l’univers, etc.

1) On appelle W le rapport des densités r / r _limite . Calculer pour W = 1   la fonction r(t) donnant le rayon d’un volume donné d’un univers en expansion.

2) Calculer le temps to écoulé depuis l’origine pour une valeur donnée de H_o.

On peut calculer les solutions de l’équation du mouvement pour E * 0, il faut résoudre l’équation :

 E = m²/2  -  GMm/r                                                                                  (6.2-6)

On exprime d’abord l’énergie totale E_o au temps to (présent) :

En remplaçant M par r_oV_o =  4p r_o r_o³ /3 et la vitesse v par H_o r_o on a :

 E_o = m H_o² r_o²/2  -  4p Gr_o r_o² m  /  3

 E_o = r_o² m (H_o²/2  -  4p Gr_o/3 )

On exprime r_o en fonction du rapport “densité / densité limite” :

 Définissons :   W_o == r_o / r_lim

r_o = 3 W_o H_o² / 8? G    =>    E_o = r_o² m (H_o²/2  -  W_o H_o² /2 )

                                               E_o = r_o² H_o² m (1- W_o) /2                                     (6.2-7)

On exprime ensuite l’énergie totale E pour un temps t  quelconque, en partant toujours de l’équation (6.2-6) :

 E = m [ (dr/dt)2 - 2 GM/r ] /2

La masse totale M est ne varie pas au cours du temps, on peut l’exprimer par roVo = 4? ro ro3/3 comme précédemment :

 E =  m [ (dr/dt)² - 8? G r_o r_o³/ 3r ] / 2
 E =  m [ (dr/dt)² - W_o H_o²  r_o³ / r ] / 2

On définit les variables sans dimension : D* = r / r_o   et     t* = H_o t

 E = m [ r_o² H_o² (dD*/dt*)² - W_o H_o²  r_o²/D* ] / 2

 E = m r_o² H_o²  [ (dD*/dt*)² - W_o/D* ] /2                                                         (5.2-8)

 Sachant que l’énergie est constante, on égalise (5.2-7) et (5.2-8) et l’équation à résoudre devient :

 (dD*/dt*)2 - W_o/D*  =  1 - W_o                                                                        (5.2-9)

On fait les changements de variables suivants :

 x = D*   |1-W_o|  / W_o    t = t* | 1-W_o|^3/2 / W_o

Et l’équation devient :

 |1- W_o|  (dx/dt)² - |1- W_o|  / x = 1- W_o

Si W_o > 1 (densité supérieure à la densité critique) on a :

 (dx/dt)² - 1/x = - 1

Et si W_o < 1 (densité inférieure à la densité critique) on a :

 (dx/dt)² - 1/x = + 1

Le cas où W_o = 1 avait été résolu dans un exercice précédent.

En séparant dx  et dt on obtient :

 dt = dx [ (x / 1 ± x) ] ^1/2

 t = * [ (x / 1 ± x) ] ^1/2  dx Les conditions aux limites sont x = 0 pour t = 0.

On fait les changements de variables suivants :
x = sin² h/2  pour le cas où W_o > 1 car l’expansion sera limitée et x < = 1
x = sh² h/2  pour le cas où W_o < 1 car l’expansion sera illimitée.

On a pour le cas  W_o > 1 :         dx = d (sin² h/2)      = d (1 - cos h) /2      = (1/2) sin h dh
 t = (1/2)* [ sin² h/2 / (1 - sin² h/2) ]^1/2  sin h dh
 = (1/2)* [ (1 - cos h) / (1+ cos h) ]^1/2  sin h dh
 = (1/2)* [ sin² h (1 - cos h) / (1+ cos h) ]^1/2  dh
 = (1/2)* [ sin² h (1 - cos h)² / (1- cos² h) ]^1/2  dh
 = (1/2) * [ (1 - cos h)²  ] ^1/2  dh
 = * dh/2 - * cos h  dh/2

On a donc une solution paramétrique pour W_o > 1 :
 x = (1 - cos h) /2      et     t = (h - sin h) /2

C’est une cycloïde : la courbe que parcourt un point à la périphérie d’une roue qui avance sur une route.    Par un calcul similaire dans le cas où W_o < 1, on a :

 x = (ch h  - 1) /2       et      t = (sh h - h) /2

6.3 Le rayonnement cosmologique fossile.

La galaxie la plus lointaine dont on a pu mesurer le spectre est à z = 5,3. Détecte-t-on des objets  plus lointains encore ? Oui : un objet particulier à z = 1000 ! C’est le rayonnement cosmologique fossile ; il présente un spectre de corps noir à 2,7 K, c’est à dire avec un maximum d’émission dans le domaine radio millimètrique.

Le rayonnement cosmologique est loin d’être un objet ponctuel : il occupe tout le ciel, sur 4? stéradians : il est quasi isotrope. L’existence de ce rayonnement a été prédite par Gamow en 1948 et par Dicke  dans les années 1965 puis détectée par hasard par Arno Penzias et Robert Willson. Son origine est une zone d’hydrogène à haute température (2700 K) qui émet un rayonnement de corps noir dont l’intensité en fonction de la fréquence et de la trempérature s’écrit :

Si l’on décale un spectre de corps noir par effet Doppler, cela revient à appliquer une affinité sur l’axe des longueurs d’onde. Dans ce qui suit, conformément à la convention en cosmologie, l’indice o correspond à ce qui est observé à l’instant présent, Le décalage spectral change une fréquence n à l’émission en no à la réception.  Avec cette convention le décalage spectral Z est défini par :

On observe depuis la terre un spectre de corps noir à une température apparente T_o :

Exprimé en fonction de la fréquence d’origine n ce spectre devient :

Le spectre émis est donc lui aussi un spectre de corps noir, mais affaibli en intensité d’un facteur (Z+1)³ , et pour une température T reliée à T_o  par  la relation T = T_o (Z+1) :

Le corps noir observé à 2.7 K correspond à une température à l’émission de 2700 K s’il est à une distance Z = 1000. Cela signifie-t-il que nous sommes entourés d’une gigantesque bulle à 2700 K ? Pas exactement. Ce que nous observons se situe dans le passé.  Z correspond à une distance, à un changement de température, mais aussi à un changement d’âge et de rayon de l’univers.

 1 + Z    =  n / n_o  =    T / T_o  =    r_o / r

T_o et n_o sont respectivement la température et le rayon de courbure de l’univers pour l’instant présent.
Si t est l’instant où  un objet de température T a émis le rayon lumineux de fréquence n, que nous observons maintenant au temps to à la fréquence n_o , r est le rayon de courbure de l'univers à l’instant t.

Le changement de température dû à Z va plus loin qu’un simple facteur d’échelle sur le spectre de Planck : on peut le considérer comme un effet de détente adiabatique de l’univers, causé par son expansion. A l’époque de l’émission du 3K l’univers était de petit rayon de courbure et la matière qu’il contient était “comprimée”. Par son expansion le contenu de l’univers s’est refroidi depuis, de même qu’un gaz se refroidit lorsqu’il se détend. Sa température actuelle est donc environ un millième de celle qu’il avait à z = 1000.

L’hydrogène s’ionise et devient opaque aux photons s’il est à une température T > 2700 K. Pour z>1000, l’hydrogène, constituant principal de l’univers à cette époque, est à une température supérieure à 2700 K et nous cache tout objet plus lointain (plus ancien). De même, à cause de l’ionisation de l’hydrogène qui la constitue nous ne voyons que la photosphère et pas l’intérieur des étoiles.

Cartes planisphères faites à partir des données du satellite COBE du rayonnement cosmologique fossile, à trois fréquences différentes. L'échelle des couleurs correspond à des fluctuations de température du spectre de corps noir correspondant, en micro Kelvins.

L’analogie entre l’univers jeune et l’intérieur d’une étoile va plus loin qu’un simple effet sur le libre parcours moyen des photons. A des temps plus anciens, pour des rayons de l’univers encore mille fois plus petits (Z=106 ), le gaz primordial atteignait des températures suffisantes pour donner lieu à des réactions de nucléosynthèse. Une partie de l’hydrogène primordial s’est transformé en hélium : de l’ordre de 15%. Le processus s’est arrêté car le milieu s’est refroidi à cause de l’expansion. Une expansion moins rapide aurait fait disparaître tout l’hydrogène primordial et le devenir de l’univers en aurait été bouleversé : plus d’étoiles...

De la proportion d’hélium dans le mélange primordial H-He, on peut déduire la durée de la phase de nucléosynthèse “primordiale”, vite arrêtée par le refroidissement dû à l’expansion, et donc le taux d’expansion à cette époque. On estime proportion d’hélium dans le mélange primordial à partir des nuages de gaz n’ayant pas encore été contaminés par des éléments venant de la nucléosynthèse stellaire. C’est une mesure difficile.

Peut-on détecter des objets à z > 1000 ? On le pourrait avec un rayonnement pour qui le milieu de cette époque serait transparent : les neutrinos ou bien les ondes gravitationnelles par exemple. Pour le moment on en est loin : on arrive juste à détecter les neutrinos du coeur du soleil. On ne dispose pas encore (1998) de détecteur direct d’ondes gravitationnelles.

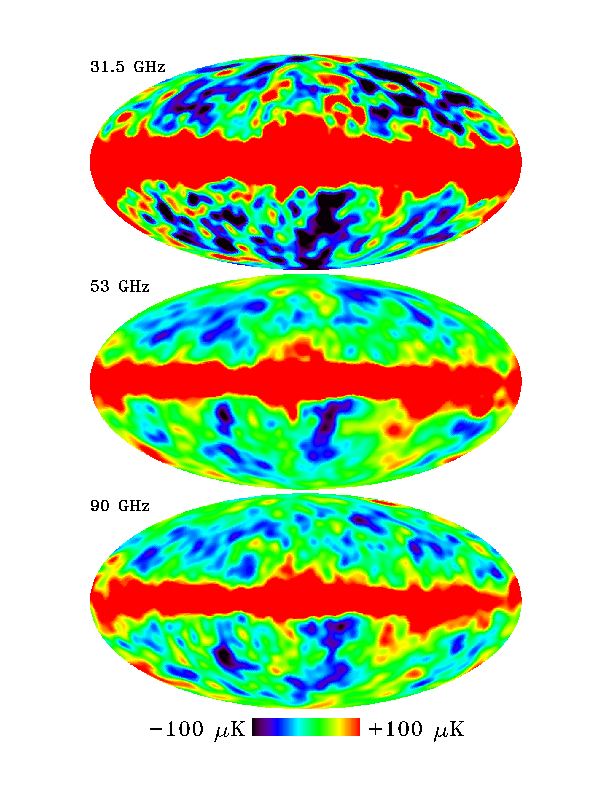
Le satellite COBE a mesuré de très légères (10- ⁵) anisotropies du 3K à l’échelle de 10° d’angle et confirmé une dissymétrie globale due au mouvement relatif de la terre (et du soleil, et de la galaxie) à 600 km/s par rapport au référentiel du 3K.
 
 

7.1 Approche intuitive de la relativité générale

Après avoir exploré le contenu de l’univers, nous allons nous intéresser au contenant pour tenter d’expliquer certaines de ses propriétés. La gravitation est l’interaction principale aux très grandes échelles. Elle est décrite par la relativité générale, extension de la relativité restreinte aux référentiels en accélération dont les deux principes de base sont :

a) Localement, en l’absence d’accélération ou de champ de gravitation la relativité restreinte s’applique.
b) Principe d’équivalence : il n’y a pas de différence (localement) entre une accélération et un champ de gravité : masse inerte = masse grave.

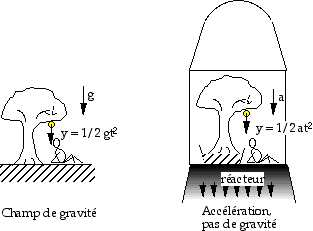
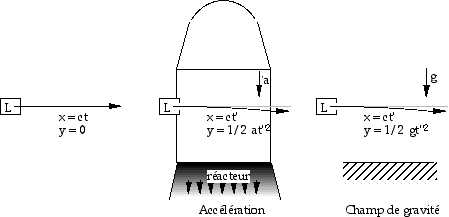
ans un référentiel en accélération et hors de tout cha;p de gravité (dessin de gauche) le mouvement de la pomme est accéléré et suit les mêmes lois que dans un champ de gravité (dessin de droite).

L’identité entre gravité et accélération concerne aussi le mouvement de la lumière : La lumière se propage en ligne droite. Ce mouvement est rectiligne dans un référentiel (x, y, t) non accéléré  (Galiléen), mais vu d’un référentiel accéléré (x’, y’, t’) il n’est plus rectiligne.

En effet un photon met un temps t fini pour parcourir une distance x donnée (t = x/c) et pendant ce temps l’origine du référentiel accéléré s’est déplacée dans une direction y de : y = 1/2 gt². Mesuré dans le référentiel en accélération le photon a parcouru une distance selon y’ :  y’ = -1/2 at².

7.2 action des masses sur la lumière.

Un champ de gravité étant équivalent localement à une accélération, il a d’après la théorie de la relativité générale le même effet de courbure sur la lumière. On observe en effet ce phénomène lorsque la lumière des étoiles passe à proximité du soleil.

our un observateur à grande distance,le champ de gravité associé à la masse M du soleil a modifié la direction du rayon lumineux d’un angle :

 q = 4GM/rc²

G est la constante de la gravitation, M est la masse créant le champ de gravité.
r est la distance minimale au centre de la masse, c est la vitesse de la lumière.

exercice :   Lorsque la lumière des étoiles passe à proximité du soleil, les voit-on plus près du soleil ou plus écartées de celui-ci ?
 

7.3 Lentilles gravitationnelles et arcs cosmiques

Toute masse dévie les rayons lumineux et agit comme une “lentille gravitationnelle”. Si des conditions d’alignement sont présentes, il peut y avoir formation d’images, mais celles-ci ne sont pas stigmatiques : elles ont généralement une forme en arc de cercle. On observe des images gravitationnelles de galaxies et quasars lointains formées par la masse de galaxies ou d’amas plus proches sur la ligne de visée.

7.4 Courbure de l’espace

La lumière suit le plus court chemin d’un point à un autre. Ceci reste vrai même si son trajet est courbe. Si dans un espace donné le plus court chemin d’un point à un autre est une courbe, c’est que cet espace lui-même est courbe. La présence de masse courbe donc l’espace.

On peut facilement se représenter un espace à deux dimensions courbes (de courbure positive) sous la forme de la surface d’une sphère. On fait mentalement une opération de “plongement” de cet espace à deux dimensions courbes dans un espace Euclidien à trois dimensions. On peut se représenter de la même façon un espace à deux dimensions de courbure négative sous la forme d’une selle de cheval ou du terrain entourant un col en montagne. Le plus court chemin d’un point à un autre en restant sur ces surfaces est une courbe appelée géodésique. Par exemple sur la surface de la terre c’est un arc de grand cercle.

Notre espace n’est pas à deux mais à trois dimensions, courbées localement et globalement par la masse qu’il contient. Pour se le représenter il faudrait le plonger dans un espace Euclidien à quatre dimension (à 5 si l’on rajoute le temps). S’il était l’analogue à trois dimensions de la surface d’une sphère ce serait une 4-sphère. Le centre d’une 4-sphère n’est pas un point de cet espace, de même que le centre d’une 3-sphère (sphère normale) n’appartient pas à sa surface.

Périmètre d’un cercle :

La courbure de notre espace dépend de son énergie totale, donc du rapport densité sur densité limite :

W_o = r_o / r_limite

Si W_o  > 1  l’espace est courbé positivement et de volume fini
Si W_o  < 1  l’espace est courbé négativement et de volume infini

7,5 Métrique de Friedmann-Robertson -Walker

C’est une des métriques utilisées en cosmologie. On appelle métrique un élément de longueur qui reste de même valeur quelle que soit l’orientation du repère dans lequel on la représente. Dans un espace Euclidien c’est :

 dl² = dx² + dy² + dz²                                                                                  (7.5-1)

Voici la même métrique exprimée en coordonnées polaires :

 dl²   =  dr²    +   r² dq²    +   r²  sin² q df²                                                  (7.5-2)
 
 

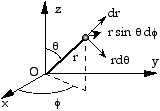
Pour passer d’une métrique dans un espace plan à celle d’un espace courbe, commençons par deux dimensions. Pour un repère d’origine O dans le plan :

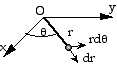
Pour un repère d’origine O dans un espace à deux dimensions de courbure positive (la surface d’une sphère), on peut exprimer r en fonction du rayon de courbure R de cet espace, et de l’angle a au centre tel que  r = Ra (voir dessin suivant). La métrique devient :

 dl²  =  R²  da²   +   R²  sin² a dq²

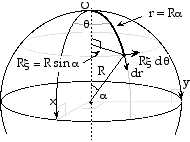
Dans cet espace, c’est la corde  R sina  et non la longueur de l’arc  Ra  qui entre en jeu pour le terme orthogonal à dr  dans l’expression de la métrique.

En définissant    x = sin a,    la métrique devient :      dl² = R² (da²   +   x² dq² )

On peut exprimer  da²  en fonction de   dx²  en utilisant les relations :

x = sin a                      =>         dx = cos a da
 da² = dx² / cos²a      =>       da² = dx² /(1 - x²)

on a finalement :

 dl²  = R² [ dx² /(1 - x²)  +  x² dq² ]                                                         (7.5-4)

Passons maintenant à un espace à trois dimensions courbes. On ne peut plus le représenter facilement par un graphique, mais on peut exprimer sa métrique en ajoutant un terme orthogonal aus deux autres, par une expression semblable à celle de la métrique d’un espace 3-D Euclidien (7.4-2) :

  dl²  = R²  [  dx² /(1 -x²)  +   x² dq² +   x² sin²q  df² ]                             (7.5-5)

Dans un expace à courbure quelconque, le coefficient a des termes orthogonaux à dr doit être remplacé par x où selon la courbure :
 

L’expression de la métrique devient :

 dl²  = R²  [  dx² /(1 -k x²)  +   x² dq² +   x² sin²q  df² ]                                  (7.5-6)

avec k valant respectivement 1, 0, ou -1 selon que la courbure est positive, nulle ou négative. En généralisant à un espace-temps courbe, on a :

 ds²  = c² dt² - dl²       =>
 ds²  = c² dt² -   R²  [  dx² /(1 -k x²)  +   x² dq² +   x² sin²q  df² ]                   (7.5-7)

C’est la métrique de Friedmann-Robertson-Walker.

1) calculer la circonférence d’un cercle dans un espace 2-D à courbure positive uniforme.
2) calculer la surface d’une 3-sphère dans un espace 3-D à courbure positive uniforme.
2) calculer le volume de la “peau” à 3-D d’une 4-sphère à courbure positive uniforme.

On peut maintenant se représenter l’expansion de l’univers, non pas comme l’augmentation de rayon d’une 3-sphère englobant un certain volume, mais comme l’augmentation du rayon d’une 4-sphère, notre espace étant la “surface” à trois dimensions de cette 4-sphère.

Retrouver la loi de Hubble pour des points fixes dans une 4-sphère dont le rayon R(t) varie en fonction du temps.

En considérant l’expansion observée de l’univers comme un accroissement de son rayon de courbure et non plus comme une déplacement des objets qu’il contient, on résout un certain nombre de problèmes. Par exemple on avait vu précédemment que la vitesse d’expansion était infinie à l’origine, ce qui n’était pas conforme à la relativité restreinte. Maintenant on voit que le vecteur vitesse d’expansion n’a pas de composante supérieure à c dans notre espace (elles sont même nulles).

Le même raisonnement tient pour des espaces courbes non clos.

7.7 Évolution du rayon en fonction du temps

L’équation qui régit le rayon d’un espace à trois dimensions courbes tel une 4-sphère ressemble à l’expression (7.5-2), C’est la relation de Fridmann Lemaître :

 R ^{- 2}   (dR/dt)² - 8 p G r(t) / 3 = - R ^{- 2} c²                                                          (7.7-1)

On peut comparer cette expression à l’équation (6.2-5) de l’approximation Euclidienne qui donnait pour une galaxie de masse m :

H_o²  - 8 p G rm_o / 3 =  2 r ^{- 2}  E / m

dans un espace en expansion courbe de rayon R on peut remplacer H_o  par :

 H_o = 1/R  (dR/dt)          voir l’exercice 7.1 :”Hyper gonflé”

L’’équation (7.2-5) deviendrait alors :

 R ^{- 2}   (dR/dt)² - 8 p G r_mo /3 =  2 r ^{- 2}  E / m

On voit que les équations  (6.2-5) et (7.7-1) se ressemblent. Seul le second membre diffère. Pour résoudre l’équation (7.7-1), on considère que la masse M contenue dans l’univers est constante donc la densité r(t) varie selon :

r(t) = M/V(t)

Le volume V(t) de l’univers est celui de la 4-sphère, il vaut :

 V(t) = 2p² R³(t)

L’équation (6.6-1) devient :

  (dR/dt)² /2  -  2 G M / 3pR  =  c²/2                                                         (7.7-2)

Si l’on fait les changements de variables suivants :

 x = R (3p c² / 4GM)
 t = t ((3p c³ / 4GM)

On retrouve la même équation que le cas traité précédemment d’un volume borné dans un espace Euclidien :

 (dx / dt)² - 1/x = - 1

Avec pour solution :

 x= (1 - cos h) /2      et     t = (h - sin h) /2

Dans le cas d’une 4-sphère de rayon R croissant à la vitesse dR/dt et contenant une masse M, quelle valeur maximale atteint son rayon ? Quel est le temps écoulé entre deux instants où R = 0 ? Calculer numériquement pour M = 10 24 masses solaires.

Imaginez un univers en expansion si rapide que...
Deux personnes sont séparées initialement par une distance l0 . L’une est immobile en A, l’autre marche à sa rencontre depuis le point B. Elles voudraient se rencontrer en A,  mais leur univers étant en expansion, il a tendance à accroître la distance qui les sépare. La personne partie de B pourra-t-elle arriver en A, donc vaincre l’expansion?
Pour résoudre le problème, faites une coupe de l’univers, supposé être la “surface” à trois dimensions courbes d’une 4-sphère, par un plan contenant son centre. On obtient un cercle, espace à une dimension courbe. L’expansion est la conséquence de l’accroissement du rayon R(t) de l’univers (voir figure).

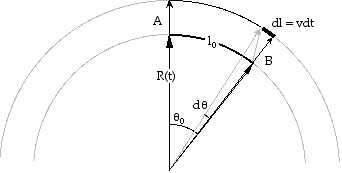
1) Exprimez l’angle q_o  (séparation initiale entre A et B) en fonction de R(t) et  l_o .
2) On considère que l’expansion de cet univers suit la loi :    R(t) = at^2/3 ,
où a est une constante. Montrez que    dq  = v a^-1 t ^{- 2/3} dt.

3) Le départ de B se situe à un temps t_o > 0 et le déplacement se fait à vitesse v constante. Exprimez l’angle parcouru q en fonction de t, t_o , a et v.

4) Dans cet univers, la personne partie de B arrivera-t-elle en A, et si oui au bout de combien de temps ? Exprimez le résultat en fonction de q_o, t_o , a et v.

5) On prend maintenant v=c (cas de la lumière), on se place au temps t. Quel est l’angle q parcouru par des photons partis de B au temps t_o si t_o = 0 ?

6) Quelle est la distance l parcourue par ces mêmes photons au temps t ?

7) Cette distance est la distance maximale jusqu’à laquelle on peut voir dans un univers d’âge t : l’horizon cosmologique. Pourquoi ne peut-on pas voir plus loin?

8) L’horizon cosmologique se déplace à une vitesse superluminique (donner sa valeur) pour les hypothèses de départ de l’exercice. Cette vitesse entre-t-elle en conflit avec la relativité restreinte ? Expliquez.

 7.8  Métrique de Schwarzschild

C’est un exemple de métrique dans un espace-temps courbe. Par comparaison, lamétrique de Robertson-Walker présentée au chapitre précedent ne prenait pas en compte la courbure du temps.

Pour un espace-temps “~Euclidien” on a la métrique de la relativité restreinte :

 ds²  = c²dt²  - dx² - dy² - dz²

Voici cette même métrique exprimée en coordonnées polaires :

 ds²  = c²dt²  - dr²   -   r²dq²   -   r² sin²q df²

Nous allons maintenant placer une masse en un point de l’espace et  étudier ses effets sur la métrique. La présence d’une masse courbe l’espace-temps. L’élément invariant dépend alors de la courbure de cet l’espace-temps et ne garde pas la même expression que ci-dessus. Dans le cas simple où la masse est à symétrie sphérique, (métrique de Schwarzschild) l’élément invariant s’exprime en coordonnées polaires avec pour origine le centre de la masse :

 ds² =  (1 -  2GM/rc²) c²dt²  - (1 -  2GM/rc²) ^-1 dr²   -   r²dq²   -   r² sin²q df² .
 
 

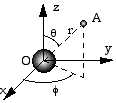
Si l’on reste dans le plan x, y  on a q = p/2 et la métrique se simplifie :

 ds² =  (1 -  2GM/rc²) c²dt²  - (1 -  2GM/rc²) ^-1 dr²   -   r² df² .

En définissant r_o = GM/c² cela donne :

 ds² =  (1 -  2 r_o/r) c²dt² - (1 -  2 r_o/r) ^-1 dr²    -   r² df² .

La vitesse s’exprime par :

v = ds_r /ds_t e_r +  ds_f/ ds_t e_f

ce qui donne dans cette métrique :

 v =  - (1 -  2 r_o/r) ^-1 (dr/dt) e_r  -   r  (1 -  2 r_o/r)^-1/2  (df/dt)  e_f

L’énergie :

 E = g m c ² (1 - 2 r_o/r ) ^1/2

avec g = (1 - v² / c² )^-1/2.

Le moment cinétique :

 L = g m r ²  (1 -  2 r_o/r )^-1/2 df / dt .
 

 7.8. Mouvement d’une masse dans un champ de gravité :

 g = (1 - v² / c² )^-1/2       =>      v² = c² (g² - 1) g^-2

En reprenant l’expression de la vitesse il vient :

 c² (g² - 1) g ^{- 2}  =  (1 -  2 r_o/r ) ^{- 2}  (dr/dt)²   -   r² (1 -  2 r_o/r )^{- 1} (df/dt)²

r²  (df/dt)² = (1 -  2 ro/r) L² / g² m² r² .

En définissant    u = 1/r     cela donne :

r²  (df/dt)² =  u² (1 -  2 u r_o) L² / g² m²

 dr/dt = (dr / du) (du / df) (df / dt)  =  - (du / df) (1 -  2 u r_o)^1/2  L / g m ,

d’où

 c2 (g² - 1) g ^{- 2}  = (du / df)²  (1 -  2 u r_o) ^{- 1} L² / g² m²  + U² L² / g² m² ,

 (du / df)²  + u² (1 -  2 u r_o) = m²  c² L^{- 2}  (g² - 1) (1 -  2 u r_o)

                                               = m²  c² L^{- 2}   [ (E² m^{- 2} c^{- 4})  -  (1 - 2 u r_o) ] .

En dérivant par rapport à f on trouve, puisque E est constant :

 d²u / df²  + u² (1 -  2 u r_o) -  r_ou²  = m² c² L^{- 2} r_o

 d²u / df²  + u  =  Gm² M + 3 G M u² /c ² .

C’est l’équation du mouvement classique avec en plus le terme : 3 Gu² M/c ² .

Ce terme est responsable entre autres de l’avance du périhélie de Mercure. On peut aussi appliquer cette équation aux photons en prenant m = 0 :

 d²u / df²  + u  =   3 G M u² / c ² .                                                                         (7.8-1)

Dans un champ de gravité pas trop intense, le terme “perturbateur” :

 3 u² G M / c²     est très petit.

On peut donc remplacer u dans ce terme par uo , solution de

 d²u_o / df²  + u_o = 0 .

On trouve : uo = cos (f - f_o)/D       =>       r_o = D / cos (f - f_o)

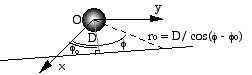
Avec D = constante, c’est l’équation d’une ligne droite passant à une distance minimale D de l’origine : trajet rectiligne d’un photon dans une métrique Euclidienne.
L’équation (7.8-1) devient :

d²u / df²   + u = 3  cos² (f - f_o) D^{- 2} G M c^{- 2} .                                 (7.8-2)

On définit :

 U =  u -  3/2  D^{- 2} G M c^{- 2}

 avec   y = f - f_o .

Cela donne l’équation :

d² U / d y²  + U = 3/2  cos² y ,                                                          (7.8-3)

qui a pour solution :

 U = D- 1 cos y   -   D^{- 2} G M c^{- 2} cos²y  /2 ,
 u = D- 1 cos y   +   D^{- 2} G M c^{- 2} (cos²y  +  2 sin²y) .

Si l’on passe en coordonnées cartésiennes  (X = r cos y ; Y = r sin y) on a :

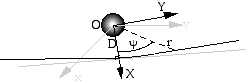
X = D - D^{- 1} G M c^{- 2} (X²  +  2 Y²)/ ( (X² + Y²) ^1/2  .

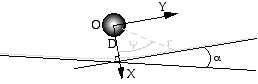
Si l’on prend Y très grand devant X on trouve les assymptotes de la courbe :

 X = D ±  2 Y G M / D c² ,

et l’angle entre les deux assymptotes vaut :

 a = 4 G M / D c² .
 
 

Confirmations de la relativité générale :

• La mesure d’Eddington en 1919 (déplacement radial apparent de 1.75 “ des étoiles vues près du bord solaire lors d’une éclipse).

• l’avance du périhélie de Mercure.

• mesures  directes des variations de l’écoulement du temps causées par le champ gravitationnel terrestre et solaire.

• observation de l’accélération de la période orbitale du pulsar double PSR 1913+16, qui correspond à une perte d’énergie par émission d’ondes gravitationnelles.

Un quasar à z = 0,2 et une galaxie à z = 0,1 sont sur la même ligne de visée. On voit deux images symétriques du quasar, décalées d’un petit angle q par rapport à l’image de la galaxie déflectrice.

a) Donner l’expression puis la valeur des distances du quasar et de la galaxie en question.

b) Donner l’expression de la masse de la galaxie (supposée ponctuelle) responsable de la déviation des rayons issus du quasar.

c) Donner une valeur numérique de cette masse, sachant que les images du quasar sont à un angle q = 1” de l’image de la galaxie.

d) Maintenant, on prend un cas un peu plus général: la galaxie déflectrice et le quasar ne sont pas parfaitement alignés. Les distances sont toujours z = 0,2 pour le quasar et 0,1 pour la galaxie.

1) calculer l’angle de déviation d’un rayon passant à une distance r minimum de 1.5 rayon solaire du centre du soleil.

2) Donner en fonction de r, la distance D du point F où des rayons initialement parallèles et passant à une distance r du soleil se rejoignent (voir schéma). Calculer la valeur de D, correspondant à r = 1.5 rayon solaire.

3) Y a-t-il une valeur minimale et/ou une valeur maximale de D ? si oui, la ou les donner.

4) La “lentille gravitationnelle” formée par le soleil et focalisant les rayons en F est-elle de bonne qualité optique ? Pourquoi ?
Est - elle achromatique ? (une lentille achromatique garde les mêmes caractéristiques quelle que soit la longueur d’onde pour laquelle on l’emploie).

5) Si l’on se plaçait au point F de convergence, à la distance D en aval du soleil sur le trajet de la lumière provenant d’une étoile lointaine supposée à l’infini, comment verrait-on cette étoile ?

6) Si l’on fait passer un rayon supplémentaire à la distance r + dr du soleil au lieu de r, à quelle distance minimale dx passe-t-il du point F ?

7) Quel décalage dr peut-on tolérer pour que les rayons tombent dans un cercle de 100 mm de diamètre centré sur le point F ?
A titre d’information : la diffraction étale le point d’arrivée des rayons en F sur une tache d’environ 100 mm de diamètre pour la lumière visible. Cela a été calculé en utilisant une ouverture annulaire de 1.5 rayon solaire dans les conditions du problème, on ne vous demande pas de faire ce calcul.

8)  Quel est le rapport entre la surface d’une tache de rayon dx autour du point F  et la “surface collectrice” d’où proviennent ces rayons :  une couronne de rayon r et de largeur 2 dr ? Faire un schéma.

9) L’énergie étant conservée entre la surface collectrice et la tache focale, quel est la rapport d’amplification de brillance ? Donner une valeur numérique pour dx = 50 mm et r = 1.5 rayon solaire. Cela permettrait-il d’observer des objets faibles ? On suppose que l’on a masqué le soleil par un système type coronographe.

Corrigé des exos (en format pdf)

Page précédente

Ouvrages ayant servi à la rédaction de ce poly, et lectures conseillées :

Franck H. Shu : “The physical Universe”, University science books.
A. Mazure, G.Mathez, Y.Mellier : “Chronique de l’espace temps” , Masson.
J.P.Perez, N. Saint Circq-Chéry : “Relativité et quantification”, Masson.
Laurent Nottale : “Towards a theory of scale relativity”, World Scientific.