
Galaxies et Cosmologie (page 1)
© 2000 L.Koechlin
DEUG 2 ème année, SMA10 Université Paul Sabatier
Enseignant : Laurent Koechlin
Ce cours fait suite au cours de physique stellaire et planétaire fait par Peter von Ballmoos
Table des matières :
Dans cette page
Unités, Notations, Constantes, alphabet
1. Echelles et distances cosmologiques
5. Structure à grande échelle
6. Isotrope ou Anisotrope?
7. Gravitation et courbure
Corrigé des exos (en format pdf)
Les unités utilisées ici sont celles du Système International. : mètre , kg, s, et quand c’est nécessaire, d’autres unités spécifiques à l’astrophysique.
Constantes d’usage fréquent dans les exercices du poly.
| Vitesse de la lumière | c | 2.99 792 458 10 8 m.s- 1 | (par définition) |
| Constante de Planck | h | 6.626176 10 - 34 J.s | |
| Cste de la Gravitation | G | 6.67 10 - 11 m 3.kg- 1.s- 2 | |
| Cste de Boltzmann | k | 1.380662 10 - 23 J.K- 1 | |
| Cste de Hubble | H0 | 70 km s- 1 Mpc- 1 | (valeur imprécise) |
| charge de l’électron | -e | -1.6021892 10 -- 19 C | |
| masse de l’électron | me | 9.109534 10 -- 31 kg | |
| masse du proton | mp | 1.67210 -- 27 kg | |
| masse du soleil | Ms | 1.989 10 30 kg | |
| rayon du soleil | Rs | 6.96 10 8 m | |
| puissance du soleil | Ps | 3.8 10 26 W | (totale rayonnée) |
| masse de la terre | Mt | 5.976 10 24 kg | |
| 1 Radian | = 180 / P degrés | =206 265 secondes d’arc | approx |
| Unité Astronomique | UA | 1.496 10 11 m | rayon moyen orbite terrestre |
| Année lumière | al | 9.46 10 15 m | |
| Parsec | 1 pc = 206265 UA | = 3.09 10 16 m | = 3.16 al |
Alphabet Grec
| alpha | a | A | beta | b | B |
| gamma | g | G | delta | d | D |
| epsilon | E | e | seta | Z | z |
| eta | H | h | theta | Q | q |
| iota | I | i | kappa | K | k |
| lambda | L | l | mu | M | m |
| nu | N | n | xi | X | x |
| omicron | O | o | pi | P | p |
| rho | R | r | sigma | S | s |
| tau | T | t | upsilon | U | u |
| phi | F | f | khi | C | c |
| psi | Y | y | omega | W | w |
En taille croissante des échelles, on utilise : m, UA, al, pc,
Z. Ne cherchez pas à retenir les valeurs numériques par coeur
mais sachez les recalculer si nécessaire.
Comme 1 radian = 206 265 secondes d’arc, on a :
1 pc = 206265 UA = 3.09 * 10 16 m = 3.16 al
On calcule alors z = ( l / lo)- 1 = Dl/lo
De Z on peut déduire la vitesse V de la source, en supposant que le décalage est dû à l’effet Doppler. Pour les valeurs de z petites devant 1, on peut utiliser l’approximation V = z c. Pour les valeurs de z comparables ou supérieures à 1, V est relié à z par la formule de l’effet Doppler longitudinal relativiste :
n = g (1 - b)
no
avec
b
= V/c et g = (1
- b2 ) - 1/2
où n est la fréquence : n
= c/l ; no
= c/lo

De Z on déduit la distance en faisant l’hypothèse que
l’univers est en expansion, ce qui implique une relation entre la position
d’un objet et sa vitesse d’éloignement par rapport à nous
(loi de Hubble). Z est non linéaire pour les grandes distances cosmologiques
à cause de la courbure de l’espace-temps.
Les distances des objets lointains sont obtenues indirectement par un enchaînement de mesures à plusieurs échelles dont chacune est basée sur le résultat de la précédente. Le résultat final est d’autant moins précis qu’il y a plus de maillons intermédiaires.
2.1 Maillon initial : la parallaxe géométrique.
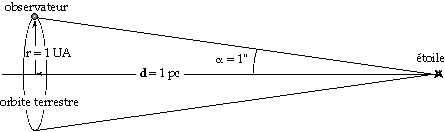
La distance des étoiles proches (<100 pc) peut se mesurer par parallaxe. On obtient la distance d d’une étoile à partir de la parallaxe (angle a dans le dessin ci-dessus) correspondant au changement de direction de visée entre deux positions de l’observateur. Dans ce schéma, l’étoile est à 1 parsec de nous et sa parallaxe est de 1 seconde d’arc : en astronomie, la parallaxe est implicitement celle correspondant à un déplacement de l’observateur de 1 rayon d’orbite terrestre.
On a la relation : r = d tan a ? d = r / tan a ?
d
= r / a (a en radians).
La distance maximum mesurable dépend de la précision avec laquelle on mesure la parallaxe. Nous disposons depuis 1995 des mesures du satellite Hipparcos qui donne une précision de 10- 3 secondes d’arc sur les parallaxes de 120 000 étoiles. Cela donne les distances avec une précision de 10 à 20 % environ à l’intérieur d’une sphère de 100 parsecs de rayon centrée sur le système solaire. A l’échelle de la galaxie (disque de 30 kpc de rayon) c’est très peu (10 - 8 en volume). La plupart des amas d’étoiles sont à des distances beaucoup plus grandes.
L’interféromètre astrométrique GAÏA, prévu pour être mis en orbite par l’Agence Spatiale Européenne donnera à partir des années 2005 des parallaxes précises à 10 - 5 secondes d’arc sur des millions d’étoiles. On couvrira alors un tiers du diamètre de notre galaxie...
Pour tout ce qui est plus loin on doit, et pour encore longtemps probablement,
recourir à des méthodes indirectes de mesure de distance.
Les mesures Hipparcos, premier maillon, permettent de calibrer en luminosité
absolue le diagramme HR des étoiles voisines du soleil.
a) Relief à l’oeil nu : Avec une précision de 4 minutes
d’arc sur une base de 10 cm. jusqu’à quelle distance voit-on le
relief à l’oeil nu ? Etablir d’abord la formule, puis donner la
distance à laquelle on a une précision de 30%.
b) Si l’on a une précision de 10 - 5 secondes d’arc
sur les mesures de parallaxe et que l’on utilise comme base le rayon de
l’orbite terrestre, jusqu’à quelle distance a-t-on une précision
relative supérieure à 10% ?
1.2.2 Deuxième maillon : distance par la relation type spectral - éclairement.
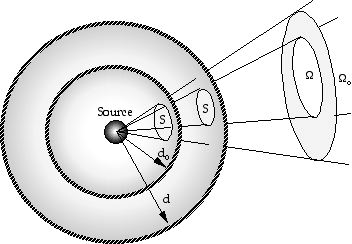
Si une source lumineuse rayonne de manière isotrope, la puissance pr reçue par un télescope de surface donnée S à une distance d de la source sera :
pr (S, d) = P S / (4pd2 )
où 4pd2 correspond à la surface de la sphère de
rayon d centrée sur la source, et P sa puissance totale rayonnée.
Calculer la puissance reçue du soleil par une surface de 1m2
au sol sur terre.
L’atmosphère terrestre atténue le rayonnement solaire
d’un facteur 1,35 par temps clair au niveau de la mer.
=> E (d) / E (do) = (do / d)2
A partir de la relation ci-dessus on peut calculer la distance d’un amas d’étoiles lointain à partir de son diagramme HR si l’on suppose que toutes les étoiles de cet amas sont à la même distance de nous, ce qui est une bonne approximation car l’amas est petit par rapport à la distance qui nous en sépare.
Dans ce qui suit
P luminosité absolue est une puissance en W ,
E (d) luminosité apparente est un éclairement
en W m - 2 .
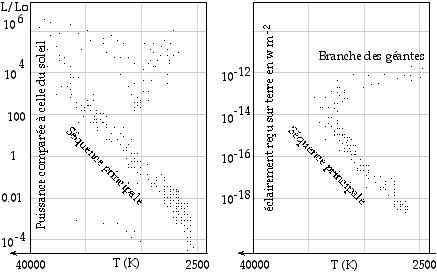
Pour le voisinage du soleil on a établi un diagramme représentant la puissance totale émise P (luminosité absolue) de chaque étoile en fonction de son type spectral. C’est le diagramme HR, caractérisé par des zones où se regroupent les étoiles: séquence principale, branche des géantes, etc. On calcule la luminosité absolue P de chacune de ces étoiles à partir de la distance d mesurée par parallaxe et de l’éclairement reçu E (d). P s’obtient en intégrant E (d) sur la surface de la sphère de rayon d :
P = 41d2 E (d)
Pour un grand nombre des étoiles de l’amas pris en exemple, on mesure le spectre et la luminosité apparente E(damas). On établit un diagramme HR de ces étoiles avec leur type spectral en abscisse et leur luminosité apparente E(damas) en ordonnée. Ce diagramme HR de l’amas ainsi établi n’est pas calibré : Pour avoir des luminosités absolues en ordonnée il faudrait connaitre la distance de ces étoiles. On y retrouve cependant des regroupements similaires à ceux du diagramme des étoiles voisines du soleil : les lois de l’évolution stellaire sont les mêmes partout. Les étoiles de l’amas sont à une distance uniforme de nous (au rayon de l’amas près) et les variations de leur luminosité apparente E (damas) traduisent les variations de leur luminosité absolue P.
On peut calibrer l’échelle en luminosité du diagramme
HR de l’amas en le “calant” sur le diagramme HR des étoiles voisines
du soleil. On en déduit alors pour chaque étoile de l’amas
sa luminosité absolue P. Comme on connait déjà l’éclairement
reçu E (damas), on déduit la distance
damas.
P = 41 damas 2 E (damas)
? damas 2 = P / 41 E (damas)
Plus riche est l’échantillon en étoiles de l’amas, meilleure
est la calibration en luminosité de son diagramme HR et sa mesure
de distance.
rouver la distance moyenne des étoiles cet amas (proches les
unes de autres par rapport à la distance qui nous sépare
d’elles). L’éclairement au sol reçu du soleil est de 1 kw
m- 2.
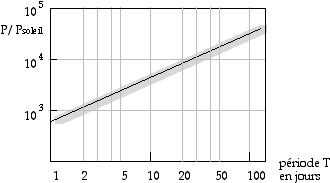
1.2.3 Troisième maillon : distance par mesure de la période
d’une céphéïde.
Quand les amas sont trop lointains on ne peut plus mesurer le spectre de leurs étoiles de la séquence principale : celles-ci ne sont pas assez brillantes. On cherche à connaître la luminosité absolue de certaines géantes très brillantes, les Céphéïdes, non plus à partir de leur spectre mais à partir de la fluctuation périodique de leur luminosité : à ce stade tardif de leur évolution ces étoiles sont variables.
E (d) /E (do) = (do / d)2 => d = do [ E (do) / E (d) ] 1/2
F(do) est l'éclairement qui serait reçu
si la source était à une distance étalon do,
d est la distance réelle de la source.
Mais il y a des poussières dans le milieu interstellaire et l’absorption rajoute son grain de sable à la formule. On a en fait :
où a est un coefficient d’absorption compris entre 0 (rayonnement
totalement absorbé, milieu opaque) et 1 (rayonnement totalement
transmis, milieu transparent).
Le coefficient a dépend de la densité de poussières
ou gaz interstellaires sur le trajet optique. On tente de l’évaluer
par le “rougissement interstellaire” qui est la signature d’une absorption
par les poussières, plus forte aux courtes longueurs d’ondes (rien
à voir avec le décalage cosmologique des raies spectrales).
L’incertitude sur la valeur de a est toujours une des causes principales
d’incertitude sur les distances.
d Céphée est la céphéïde la plus proche de la terre. Elle sert (avec d’autres) d’étalon d'éclairement pour calibrer la distance des céphéïdes plus lointaines, il est donc important de connaître sa distance précisément et de manière indépendante. C’est ce que vous allez faire, mais d’une façon originale et plus précise que par les autres méthodes. On vous donne pour cela les instruments les plus puissants disponibles actuellement.
D’abord un interféromètre stellaire optique. Avec cet instrument vous pouvez véritablement voir la forme et le diamètre angulaire des étoiles. La précision des mesures avec un tel instrument est de 5 x 10 - 5 seconde d’arc.
Ensuite vous avez un spectromètre capable de voir des raies spectrales fines et des décalages spectraux très faibles.
a) Avec le spectromètre, on observe les raies spectrales de d Céphée. A un moment donné elles sont toutes décalées vers le bleu mais un peu plus tard elles sont toutes décalées vers le rouge, puis de nouveau vers le bleu, et ainsi de suite (voir figure ci-dessous). Quelle explication voyez-vous à ce phénomène ? Que se passe-t-il précisément quand par exemple elles sont décalées vers le bleu ? On rappelle que d’une part l’étoile n’est pas double et que d’autre part le phénomène n’est pas dû à la rotation de l’étoile sur elle-même.
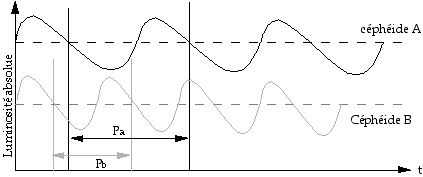
b) Voici la courbe du décalage spectral d’une raie de d Céphée en fonction du temps :
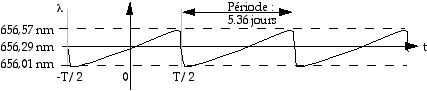
Attention, ce n’est pas exactement le même type de courbe que
pour la luminosité. Ici on va supposer que la courbe est sinusoïdale.
Pour la raie spectrale donnée en exemple on a :
l min = 656,01 nm l moyen = 656,29 nm l max = 656,57 nm
Période de variation : 5.36 jours.
On suppose que la lumière observée est issue du point
de la surface de l’étoile qui nous fait face et que l
moyen correspond à une vitesse nulle.
Quelle est la vitesse radiale maximale de la surface de l’étoile
?
c) Donner une expression analytique de cette vitesse en fonction du temps (il est conseillé de calculer la période en secondes).
d) En intégrant cette vitesse dans le temps, qu’obtient - on ?
e) Donner une expression analytique du diamètre de l’étoile en fonction du temps.
f) Quel est l’écart entre le diamètre minimum (dmin) et le diamètre maximum (dmax) de l’étoile ? Donner la réponse en m.
g) Maintenant vous prenez l’interféromètre stellaire. Celui-ci vous permet de mesurer le diamètre angulaire de d Céphée. Selon le moment où est faite la mesure, les résultats s’échelonnent entre une valeur minimum (ømin) et une valeur maximum (ømax). Donner une formule permettant de calculer la distance de l’étoile en combinant les mesures de l’interféromètre : ømin, ømax, et les résultats obtenus avec le spectromètre : dmin, dmax.
h) ømin = 1.1 x 10 - 3 secondes d’arc et
ømax = 2.1 x 10 - 3 secondes d’arc.
donner la distance de l’étoile en m, puis en parsecs. (1 pc
= 3.09 x 10 16 m).
i) donner le diamètre minimum et le diamètre maximum de l’étoile.
j) compte tenu de la précision de l’interféromètre, donner l’incertitude sur la distance (on négligera l’incertitude sur les décalages spectraux).
Question de point de vue :
Que se passerait-il si l’on mettait une céphéïde
à la place du soleil ?
1.2.4 Étalons d'éclairement et étalons de taille.
La mesure de distances plus grandes ne met pas en jeu les céphéïdes
car elle ne sont pas assez lumineuses pour être vues. Pour les galaxies
lointaines on recourt à des étalons moins précis mais
plus brillants (dans l’ordre des distances et brillances croissantes) :
• Luminosité moyenne des étoiles non variables les plus
brillantes.
• Luminosité moyenne des amas globulaires.
• Taille moyenne des régions H II (étalon angulaire).
• Luminosité des galaxies de type Sc I .
• Luminosité des supernovae à leur maximum (peut servir
d’étalon angulaire indirect :
P = 4 1 R2 s T 4
P est la puissance rayonnée (luminosité absolue).
R, le rayon de la supernova, est connu par intégration des vitesses
radiales.
s est la constante de Stéphan.
T est la température absolue de la surface de l’étoile,
déduite de son spectre.
• Luminosité moyenne des trois plus brillantes galaxies d’un
amas
• relation entre largeur d’une raie d’émission C IV et luminosité
absolue des quasars.
• relation entre la largeur spectrale de la raie O III et la luminosité
absolue dans la raie Ha pour les galaxies.
1.2.5 Distances déduites du décalage spectral
Le maillon ultime de mesure des distances est l’observation du décalage
vers le rouge (red shift) des raies spectrales. Hubble a observé
dans les années 1920 que les galaxies lointaines dont il avait pu
mesurer indépendamment la distance et le spectre avaient décalage
spectral proportionnel à leur distance.
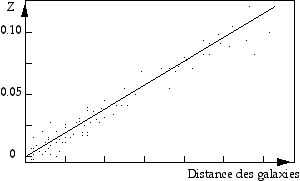
Faisant l’hypothèse que ce décalage spectral était
dû à l’effet Doppler, il en a déduit une vitesse relative
pour chaque galaxie.
v = c Æl/l = c z (pour Æl/l << 1)
Le diagramme indiquait une relation de proportionnalité entre
leur distance D et leur vitesse v :
d = v / Ho
Ho est la constante de Hubble : actuellement Ho
= 70 ± 20 km s- 1 Mpc- 1
L’unité barbare (km s- 1 Mpc- 1) vient du fait que l’on mesure
les distances en mégaparsecs et les vitesses en km/s. C’est en fait
l’inverse d’un temps.
Donner le temps correspondant à Ho- 1 .
Quelle signification physique a-t-il ?
v = g - 1 c z = g - 1 c Æl/l où g = (1 - v2/c2 ) - 1/2
z 2 = v 2 / (c 2 - v 2 )
Mais cette “vitesse” n’a pas grand sens physique et mènerait à une expression erronée de la distance si l’on gardait une relation linéaire entre vitesse et distance. On exprime directement d en fonction de z. Cette relation entre z et d pour une source lointaine dépend de la courbure de l’univers et de la façon dont on veut exprimer la distance. Pour un modèle standard on peut prendre :
d = (c /2Ho) [ (1+z) 2 - 1]
où d est la variable pour laquelle la loi E(d) /E(do) = (do / d)2 reste valable malgré la courbure de l’espace. Cette distance est appelée “distance photométrique”. A cause de la courbure de l’espace elle ne correspond pas à celle que l’on trouverait en mesurant le parallaxe, ni à celle, encore différente, que l’on trouverait si l’on pouvait mesurer le temps de trajet de la lumière.
1) Quelle est la distance photométrique d’un objet à Z
= 4 ?
2) Y a - t - il incompatibilité avec l’âge de l’univers
(15 milliards d’années) ?
Les instruments au sol donnent accès au domaines visible, Infra-rouge proche et radio, pour observer les UV, X, g, et les IR lointains il faut sortir de l’atmosphère. Il existe d’autres types d’ondes qui peuvent être émises par les objets astrophysiques : neutrinos (déjà observés), ondes gravitationelles (non encore directement observées) , et des particules cosmiques.
Constituants d’un télescope actuel :
Système de pointage,et de guidage
Monture au sol : équatoriale, alt-az, alt-alt, boule.
Système de Focalisation de la lumière.
3.1 Rappels d’optique géométrique
Relation entre focale, distance image et distance objet :
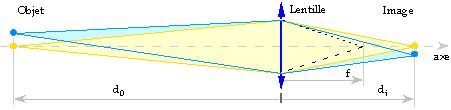
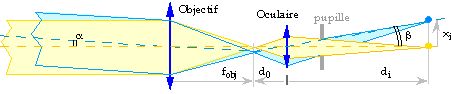
3.2 Diffraction
La diffraction limite la résolution des instruments d’observation astronomique en limitant le finesse des images : une source ponctuelle sera focalisée non en un point, mais en une petite tache (la tache de diffraction) de rayon minimum r. Pour une ouverture circulaire, on a :
r = 1.22 l f / d ce qui correpond à un angle q = r / f = 1.22 l / d
où l f et d sont recpectivement la longueur d’onde de la lumière utilisée, la focale, et le diamètre du télescope.
Rapport entre diffraction et relation d’incertitude
Il y a un lien entre la relation d’incertitude d’Heisenberg et la diffraction : prenons un photon dont on cherche à connaître, dans la direction perpendiculaire à sa propagation, à la fois la position et la quantité de mouvement.
L’incertitude sur la position du photon correspond à la taille a d’un diaphragme limitant l’étendue du faisceau qui le contient. L’incertitude sur la quantité de mouvement du photon correspond à la divergence Dq du faisceau après passage au travers de ce diaphragme.
Dx = a ; Dp = p Dq
La quantité de mouvement d’un photon vaut :
p = hn / c
Où h est la constante de Planck.
D’autre part la réponse impulsionelle d’un système optique
donne une relation entre a et Dq :
Dq = l / a
=> Dp Dx = p Dq a = p l = l hn / c = h
On retrouve : Dp Dx = h La divergence d’un faisceau peut toujours être augmentée par des aberrations mais jamais réduite en dessous du seuil de la diffraction : Dp Dx >= h.
On peut aussi facilement retrouver Dp Dx >= h à partir de la cohérence spectrale. La relation d’incertitude est une conséquence de la TF et de la nature ondulatoire des objets auxquels elle s’applique.
3.2 Effet de la turbulence sur l’indice de l’air
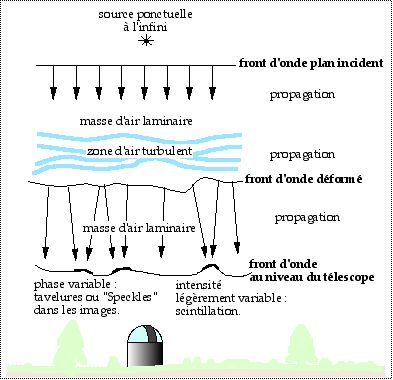
a) Calculer la différence de chemin optique L associée à la traversée d’une veine d’air “froid” de 0.25 m d’épaisseur ayant un écart en température de 1 °C avec l’air environnant : température de l’air environnant : 300 °K.
L’indice de l’air est n = 1,0002817 à l = 400 nm, et (n-1) varie proportionnellement à sa densité.
b) Cette veine d’air froid empiète sur une partie du passage
de la lumière arrivant dans un télescope. Quels sont les
effets sur les images données à l
= 400 nm?
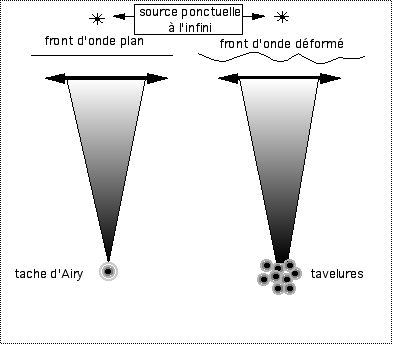
matériel nécessaire : laser+lentille (f = 5 à 50
mm) pour étaler le faisceau.
Fixer la lentille à la sortie du laser, regarder la tache du
faisceau étalé sur un écran. Prenez les précautions
nécessaires pour que le faisceau ou son reflet n’atteigne pas les
yeux de quelqu’un. Ne jamais regarder fixement l’impact sur un écran
d’un faisceau laser, même de faible puissance, s’il na pas été
étalé par une optique quelconque : DANGER !
On voit des speckles sur l’écran car les différentes parties éclairées par le laser sont des sources cohérentes entre elles et leurs amplitudes s’ajoutent, formant des interférences sur la rétine. La taille angulaire des speckles vus par l’oeil vaut :
q s = l/D où D est le diamètre de la pupille de l’oeil.
La taille angulaire de ces speckles ne dépend pas de la distance
de l’oeil à l’écran. Elle dépend par contre de D.
On peut faire varier celui-ci en plaçant un diaphragme devant son
oeil.
voir le cours de J P Perez sur la fonction de transfert en éclairage
cohérent.
expérience : Speckles en éclairage incohérent.
Matériel nécessaire :
Lampe halogène de bureau ou une autre source ponctuelle.
Cache plastique dépoli (type couverture de cahier)
Négatif sur film à grain fin des masques ci-dessous ou
à défaut trous d’épingle de ø 1 et 0.2 mm dans
du papier d'aluminium.
Se placer à plusieurs mètres de la source lumineuse pour qu’elle apparaisse ponctuelle et la regarder avec le masque ci-dessus placé contre son oeil (diapositive ou alu). On observe la fonction de transfert incohérente sans aberration. En plaçant le plastique dépoli devant le masque on introduit des distorsions de phase et crée des speckles. Comparer les speckles vus à travers le trou ø 1 mm, le trou ø 0.2 mm et les deux ouvertures rapprochées.
3.3 Optique adaptative.
Dans les techniques précédentes de reconstructions d’image,
on mesurait de plusieurs façons possibles la fonction de transfert,
dans le but de corriger les aberrations qu’elle induisait dans les images.
L’optique adaptative agir directement et en temps réel sur
la fonction de transfert, de manière à la rendre le plus
ponctuel possible. L’optique adaptative c’est en quelque sorte de la médecine
préventive, en comparaison des méthodes précédentes
qui sont “curatives”.
4.1 Structure d’une galaxie spirale
Ce sont d’immenses regroupements d’étoiles, gravitationnellement liées. Leur masse totale varie beaucoup d’une galaxie à une autre, elle est de 10 11 masses solaires en moyenne. Les galaxies ne sont reconnues comme telles que depuis 1925, date à laquelle Hubble mit un terme à la polémique entre Curtis et Shapley sur leur nature en mesurant la distance de M31 (galaxie d’Andromède) par la méthode des céphéïdes. La distance trouvée (500 kpc), indiquait clairement que celle-ci est à l’extérieur de notre galaxie (diamètre 30 kpc).
Vous détectez un céphéïde dans M31.
sa période de variation est P = 30 jours
sa magnitude apparente correspond à un éclairement au
sol de 10 - 15 W. m- 2
l'éclairement reçu au sol en provenance du soleil est
de 10 3 W. m- 2
Quelle est la distance de M31 si l’on néglige l’absorption interstellaire
?
Il y a quelque 10 11 galaxies dans les limites de l’univers actuellement observable, autant que d’étoiles dans une galaxie. Les plus courantes sont les spirales.
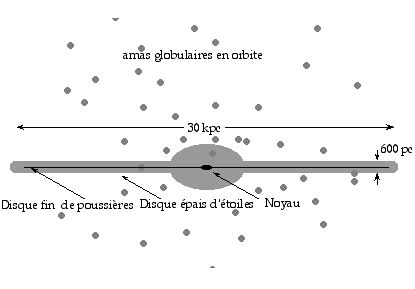
Les étoiles du disque ont un mouvement orbital autour du centre galactique (période d’environ 250 millions d’années) et un mouvement d’oscillation de part et d’autre du plan galactique. Ce mouvement d’oscillation permet de connaître le champ de gravité associé au disque (en mesurant la statistique des vitesses des étoiles) et d’en déduire la densité locale. En la comparant au nombre d’étoiles on trouve un résultat bizarre : la masse créant le champ gravitationnel est cinq fois plus élevée que la masse totale des étoiles observées. Il y a un problème de “masse manquante” que l’on retrouve à plusieurs échelles en cosmologie et que l’on explique par la présence de matière non rayonnante : gaz interstellaire, et d’autres sources de champ gravitationnel (inconnues à ce jour : masse des neutrinos ?).
Pour la partie centrale de la galaxie, les étoiles ne sont plus organisées en disque : leurs orbites semblent orientées aléatoirement. Le spectre de ces étoiles révèle une plus faible teneur en matériaux lourds (faible métallicité) que celles du disque. Elles sont en général plus âgées et leur faible métallicité vient du fait que le gaz qui les a formé n’a pas été enrichi par des générations d’étoiles précédentes. Ce étoiles sont appelées “population II”, par opposition aux étoiles récentes du disque “population I”. (Formule mnémotechnique : les étoiles de population II ont deux ans, celles de population I un an, donc plus jeunes).
On peut calculer la masse d’une galaxie à partir des vitesses radiales des nuages d’hydrogène neutre détectés en radio-astronomie dans la raie d’émission à l = 21 cm. Ces nuages sont détectables à des grandes distances du centre des galaxies et leur mouvement permet de mesurer la masse contenue à l’intérieur de leurs orbites.
1) En partant des lois de la gravitation, montrer que pour un objet de masse négligeable en orbite circulaire autour d’un objet de masse M on a :
M = v 2 r / G
où G = 6.67 10 -11 est la constante
de la gravitation.
r est le rayon de l’orbite.
v est la vitesse linéaire le long de l’orbite.
2) On mesure la vitesse radiale des nuages d’hydrogène de cette galaxie par effet Doppler sur la raie d’émission à no = 1420 MHz (lo = 21 cm) de l’hydrogène neutre.
a) La fréquence de cette raie spectrale observée dans le disque de la galaxie n’est pas la même partout. Elle se répartit entre deux valeurs extrêmes :
ng
= 1418,6 MHz sur un bord du disque
nd
= 1421,4 MHz sur le bord opposé du disque
En déduire DF / F puis DVr, où Vr est la vitesse projetée sur la ligne de visée (vitesse radiale). Finalement déduire Vr, vitesse radiale d’un bord de la galaxie par rapport à son centre. On supposera que les vitesses sont symétriques par rapport au centre de la galaxie.
b) Le disque de la galaxie est incliné d’un angle i= 60 ° par rapport au plan du ciel. Pour une vitesse réelle V dans le plan de la galaxie, la vitesse radiale Vr observée vaut :
Vr = V sin i

3) On a mesuré la distance de la galaxie et trouvé D = 600 kpc. Les nuages d’hydrogène neutre sont observables jusqu’à un écart angulaire a de 2 degrés du centre de la galaxie. Trouver le rayon de leur orbite, que l’on supposera circulaire, et la période de rotation.
4) Quelle est la masse de cette galaxie ?
A combien de masses solaires cela correspond-il ?
On peut aussi calculer la masse totale d’une galaxie à partir de la statistique de vitesses des amas globulaires qui orbitent autour. On trouve des valeurs encore plus élevées mais entachées d’incertitude car les orbites de amas globulaires ne sont pas dans le plan du disque et de ce fait assez complexes.
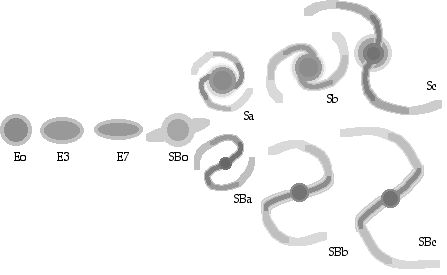
4.2 Classification de Hubble
D’autre types de galaxies que les spirales sont observées : 10% environ sont des elliptiques. Une tentative de classifications fut faite par Hubble, sur le modèle de la classification des espèces animales par les zoologistes du 19 ème siècle. Cette classification des elliptiques, spirales et spirales barrées ne correspond pas à l’évolution temporelle d’une galaxie donnée. Certaines galaxies ont des formes inclassables, dites irrégulières : c’est le résultat de collisions en cours ou récentes entre galaxies.
4.3 Évaporation et effondrement des amas globulaires
A l’intérieur d’un amas, les étoiles sont liées par leur attraction gravitationnelle mutuelle. Leurs orbites sont instables et on ne sait pas les calculer analytiquement (problème à n corps). On en fait des simulations numériques avec un nombre limité d’étoiles. On peut aussi faire une étude statistique moyennant quelques approximations :
L’énergie potentielle d’un couple d’étoiles de masse égale en interaction gravitationnelle est donné par :
Energie potentielle pour un couple étoiles : Ep = - Gm2/R
où R est la distance entre les étoiles et m leur masse individuelle. Considérons l’amas comme formé de N étoiles de masses égales, chaque étoile étant liée gravitationnellement aux N-1 autres. On a N(N-1)/2 liaisons. Mettons les distances entre étoiles toutes égales à R, l’énergie potentielle s’exprime par :
Energie potentielle pour tout l’amas : Epa = -
N(N-1) Gm2 / 2R
Le théorème du Viriel donne : Ec
= - Ep /2
Pour tout l’amas : Eca = - Epa /2
? Eca = N(N-1) Gm2 /
4R
Par ailleurs on sait que pour tout l’amas : Eca
= NmV2 /2
En mettant ces deux équations ensemble : V2
= (N-1) Gm / 2R
Ceci donne la vitesse moyenne V des étoiles dans l’amas.
Par ailleurs on peut trouver la vitesse de libération Ve d’une étoile de l’amas (par définition, si V > Ve , l’étoile s’échappe de l’amas). Prenons une étoile supposée être à une distance R du centre, elle est liée aux N-1 autres de l’amas, et elle se déplace à la vitesse de libération :
on a son énergie potentielle : Epe = - (N-1)
Gm2 / R
et son énergie cinétique : Ece =
mVe2 /2
A la vitesse de libération on a par définition : Ece
= - Epe
En mettant ensemble les expr. ci-dessus : Ve2
= 2 (N-1) Gm / R
On voit que V = Ve / 2 . Il faut cependant considérer V comme une vitesse moyenne, les rapprochements occasionnels entre étoiles se traduisent par des perturbations et des changements de direction. Leur effet cumulé sur un temps assez long crée une dispersion des vitesses qui obéit aux mêmes équations que celle des molécules dans un gaz (distribution de Maxwell - Boltzmann). Il y a une différence cependant : la queue de distribution à des vitesses V > Ve n’existe pas dans un amas ; ces étoiles sont rapidement éjectées.
Les perturbations gravitationnelles tendent cependant à rétablir
la partie à grande vitesse de la distribution, et de nouvelles étoiles
sont éjectées. Les amas ‘s’évaporent”. L’énergie
nécessaire à l’évaporation est puisée dans
le reste de l’amas : le rayon du coeur diminue. On peut estimer les temps
d’évaporation des amas en fonction de leur temps de relaxation (temps
moyen entre deux frôlements d’étoiles). Les temps d’évaporation
moyens sont de 3 * 109 ans pour un amas ouvert et
8 * 1010 ans pour un amas globulaire.
4.4 Théorème du Viriel (Clausius,
1870) .
Pour une particule de masse m et de vitesse v << c, l’énergie cinétique vaut
Ec = 1/2 mv2 .
Pour un ensemble de particules de masses mi et de vitesses vi, on a
Ec = 1/2 Smivi2 = 1/2 S pidri/dt (1)
où p = mv ; r est la position à partir d’une origine arbitraire.
Par ailleurs, l’expression de la dérivation d’un produit de
fonctions donne
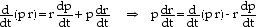 (2)
(2)
en appliquant (2) à (1), on trouve
Ec = 1/2 Sd(pi ri)/dt - 1/2 Sridpi/dt . (3)
dp/dt = F , la force appliquée sur une masse. Appliquée dans (3), cette relation donne
Ec = 1/2 Sd(pi ri)/dt - 1/2 SriFi. (4)
On va s’intéresser maintenant à la moyenne dans le temps de Ec. On va voir que le premier terme de l’expression (4) tend vers zéro quand on moyenne sur un temps infini.
Définissons G = Spi ri et g = dG/dt
Ec = 1/2 g - 1/2 SriFi. (5)
<Ec>t = 1/2 <g> t - 1/2 <SriFi> t . (6)
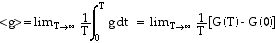 (7)
(7)
Les valeurs de G sont bornées car les pi et ri ne peuvent pas être infinis. Le facteur 1/T fait donc tendre <g> vers zéro pour T grand.
On a donc
<Ec>t
= - 1/2 <SriFi>t
= - 1/2 n .
(8)
On appelle “Viriel” la quantité
n º <SriFi> , (9)
qui est homogène à un travail. Dans le cas où les forces sont dues à un champ de gravité centré en r = 0, on va voir que le viriel correspond à l’énergie potentielle moyenne : La force appliquée sur une particule de masse m vaut
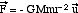 ,
(10)
,
(10)
où G est la constante de la gravitation, M la masse causant le champ de gravité et u le vecteur unité orienté de M vers m. Injectant (10) dans (9) donne
n = - S<GM mi / ri> . (11)
Or l’énergie potentielle d’une particule dans ce champ s’exprime
par
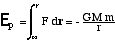 (12)
(12)
Le viriel correspond donc à l’énergie potentielle moyenne du système
n = <Ep> , (13)
et d’après l’expression (8) on trouve
<Ec> = - 1/2 <Ep> . (14)
Pour l’énergie mécanique
<E> = <Ec> + <Ep> = 1/2 <Ep> . (15)
4.5 Origine des bras spiraux
Si l’on considère que les orbites des étoiles du disque sont initialement circulaires, des instabilités peuvent se développer et les rendre elliptiques centrées. Si les grands axes de ces orbites ne sont pas alignés mais forment un angle croissant avec le grand axe, on va avoir des zones de rapprochement en forme de bras spiraux :
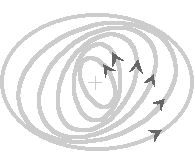
La période de rotation du soleil autour du centre galactique
étant de 250 millions d’années environ, il doit subir tous
les 150 à 300 millions d’années un taux accru de formation
d’étoiles chaudes dans son voisinage. Dans le cadre des rapprochements
(d’idées) hasardeux, les dinosaures ont disparu il y a 165 millions
d’années...
Un astronome voit d’une galaxie sous un rayon apparent g = 0,5
°.
1) Quel est le déplacement angulaire d’une étoile du
bord du disque en dix ans si la période de rotation de cette galaxie
est 250 millions d’années ?
1a) donner l’angle a vu du centre de la galaxie.
1b) donner l’angle b vu de la terre.
2) Un astronome a fait deux clichés de cette galaxie à
dix ans d’intervalle. Pourra-t-il détecter le déplacement
des étoiles dû au mouvement orbital autour du centre de masse
de cette galaxie ? (il dispose d’un télescope donnant une résolution
de 0,1”).
3) Quel est l’intervalle de temps minimum entre deux clichés
de la galaxie pour qu’il puisse mettre en évidence le déplacement
des étoiles ?
4) devra-t-il vraiment attendre aussi longtemps ? Pourquoi ?
4.6 rapports M/L
Si l’on compare le rapport Masse sur Luminosité ou “M/L” du soleil à celui d’une galaxie, on trouve une valeur supérieure à 1 :
Objet “M/L” = (Mgal/Msol)
/ (Lgal/Lsol)
Soleil : 1
Spirales : 3 à 5
Elliptiques : 10 à 20
Bien que la majorité des étoiles soient moins massives que le soleil et de ce fait aient des rapports M/L supérieurs à 1 (la luminosité d’une étoile varie fortement en fonction de sa masse) , la masse totale d’une galaxie correspond à plus que la somme des masses des étoiles vues. La masse “invisible” peut être sous forme d’étoiles non détectées : naines noires, étoiles à neutrons ou trous noirs, ou de gaz non encore formé en étoiles, ou de matière non baryonique. Elle représente de 60 à 80% de la masse totale pour les galaxies spirales.
4.7 Galaxies actives, Quasars, Jets
On appelle galaxies à noyau actif (Seyferts, BL Lac, Quasars,
QSOs) celles dont le noyau est particulièrement brillant et vu quasi
ponctuel. Le spectre contient parfois des raies d’émission larges
sur un fond continu non thermique, i.e. qui ne correspond pas à
un spectre de corps noir. Le continu du spectre est en loi de puissance,
avec une partie détectée dans les domaines g
,x et radio.
Historiquement ces objets ont été pris pour des étoiles
particulières, leur nature extra-galactique n’a été
découverte que récemment.
• BL Lac : C’est sous ce nom que les observateurs d’étoiles
variables l’ont cataloguée. C’est en fait le coeur très brillant
d’une galaxie elliptique géante, variable d’un facteur 15 à
l’échelle de quelque jours. La galaxie qui l’entoure n’a été
détectée qu’en 1975 car très peu lumineuse par rapport
au coeur. On observe plusieurs galaxies de ce type réparties aléatoirement
dans le ciel, auquel on donne le nom générique “les BL Lac”.
Elles sont aussi détectées en radio.
La variabilité rapide de ces objets donne un indice sur leur
taille maximum :
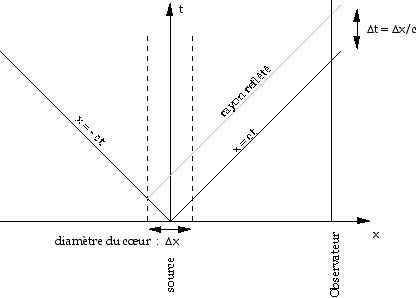
Dans ce diagramme x, t (le temps et une dimension d’espace), on choisit
les échelles en x et en t de manière à ce qu’un rayon
lumineux (se propageant à la vitesse ± c) soit représenté
par une droite de pente ± 1.
On voit qu’une source lumineuse de taille Æx qui émettrait
un flash serait vue lumineuse pendant une durée Æt = Æx
/ c .
• Les galaxies de Seyfert sont des spirales avec un coeur très
brillant, comme les BL Lac.
• Les quasars (de QUAsi StellAR) sont une autre variété
de galaxie, à noyau actif encore plus brillant que celui des BL
Lac et des Seyferts. Ce sont les objets les plus lointains détectables
(à part le rayonnement cosmologique à 3 K) on les observe
jusqu’à des distances de z = 5.
On n’observe pas de quasars proches. La raison en serait leur durée
de vie limitée, ou ce qui revient presque au même, une baisse
de puissance au cours du temps. En effet, on voit les objets tels qu’à
un temps :
t = to - d/c
où to, d et c sont: le présent,,
leur distance, la vitesse de la lumière.
Pour les quasars, d/c est une fraction non négligeable de l’âge
de l’univers. Leur temps de vie y est donc inférieur et il ne s’en
forme plus maintenant.
• Les QSOs (Quasi Stellar Objects) ne sont observés qu’en radio astronomie. Ils ont les mêmes caractéristiques spectrales (en radio) et morphologiques que les quasars mais n’ont pas de contrepartie optique détectée.
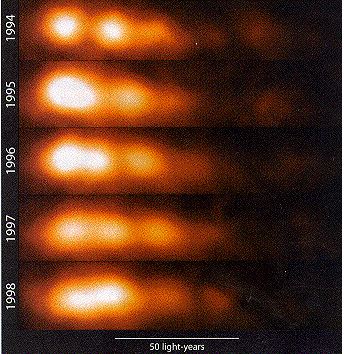
Certaines galaxies à noyau actif, dont les quasars et QSOs, sont entourées d’un ou deux jets diamétralement opposés, détectés en radio ou en optique. Certains de ces jets sont discontinus (genre signaux de fumée) et l’on observe leur déplacement apparent entre deux images prises à plusieurs années d’intervalle. Par exemple un déplacement angulaire de 4 millisecondes d’arc en trois ans pour le jet du quasar 3C273.
On approxime dans cet exercice simple les ondes radio émises par un pulsar au faisceau d’un phare de marine. Ce pulsar tourne sur lui-même à 1 tour par seconde.
a) Donner l’expression de la vitesse de passage du faisceau au niveau du système solaire. Définissez vous-même les variables nécessaires. Faites un schéma.
b) Donner la valeur numérique de cette vitesse si nous sommes à 200 parsecs du pulsar.
c) Si la vitesse trouvée est supérieure à c, cela
remet-il en cause la théorie de la relativité ? Pourquoi
?
Un exemple de mouvement superluminique observé en optique : les anneaux écho de la supernova SN 1987 A.
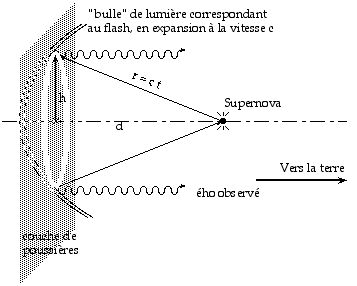
Cette étoile a “explosé” en février 1987 .
Depuis 1988 on observe des anneaux autour, dont la rayon semble croître plus vite que la vitesse de la lumière. On explique ce phénomène par l’écho du “flash” de l’étoile sur des nébuleuses de poussières situées en arrière-plan. Le rayon de l’anneau écho observé est noté h et la distance entre la supernova et les poussières notée d. On prend t = 0 à l’explosion de la supernova et t = to au moment où la lumière atteint la couche de poussières : d = c to.
Donner une expression de la vitesse apparente d’expansion de l’anneau
écho.
Mouvement superluminique observé en radio, illustré dans le “film” plus haut. Un quasar émet un nuage de gaz à la vitesse v dans une direction proche de la ligne de visée, faisant un angle q avec celle-ci.

1) Donner l’expression de la vitesse apparente va en fonction de b º v/c et de l’angle q.
2) Pour une valeur donnée de b, quelle est l’angle q donnant la valeur maximale de va .
3) Calculer les valeurs minimales de va et b pour lesquelles on a un effet superluminique.
4) Calculer va pour b = 0.9
L’énergie rayonnée dans le visible peut aller jusqu’à 10 11 Lo . On sait, grâce à leur variabilité que ces sources d’énergie sont contenues dans des volumes très petits : quelques jours à quelques mois lumière de rayon. Si la puissance dégagée provenait d’étoiles, elles formeraient un amas extrêmement dense et on peut calculer qu’il évoluerait rapidement “par évaporation” des étoiles rapides et formation d’un trou noir central supermassif (10 7 à 10 8 masses solaires pour les Seyferts, 10 9 à 10 10 masses solaires pour les quasars).
L’accrétion de matière par un tel trou noir peut être un moyen très efficace de transformer la matière en rayonnement : 70 % de rendement environ comparé à 15 % pour la fusion de l’hydrogène dans les étoiles.
On a maintenant des indications très nettes que les galaxies “normales” telles que la nôtre ou M31 (Andromède) ont aussi un trou noir supermassif central. Celui-ci n’étant plus “alimenté” en matière, rayonne très peu. On reviendra sur la physique de ces objets.
Corrigé des exos (en format pdf)