Collision term for velocity:

$\frac{\delta U_s}{\delta t} = \frac{1}{n_s m_s}\frac{\delta M_s}{\delta t}$

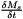with $\frac{\delta M_s}{\delta t}$ given by Schunk (1977) in the 13-moment equation:

$\begin{eqnarray*} \frac{\delta U_s}{\delta t} &=& \frac{1}{n_s m_s}\left[\sum_t n_s m_s \nu_{st} (U_t-U_s) + \sum_t \nu_{st}\frac{z_{st}\mu_{st}}{k_bT_{st}}\left(q_s-q_t\frac{\rho_s}{\rho_t}\right)\right]\\ \end{eqnarray*}$

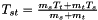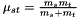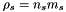with $T_{st}=\frac{m_sT_t+m_tT_s}{m_s+m_t}$ , $\mu_{st}=\frac{m_sm_t}{m_s+m_t}$ , $\rho_s = n_s m_s$ .

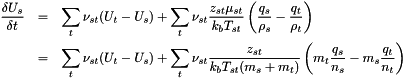
$\begin{eqnarray*} \frac{\delta U_s}{\delta t} &=& \sum_t \nu_{st} (U_t-U_s) + \sum_t \nu_{st}\frac{z_{st}\mu_{st}}{k_bT_{st}}\left(\frac{q_s}{\rho_s}-\frac{q_t}{\rho_t}\right)\\ &=& \sum_t \nu_{st} (U_t-U_s) + \sum_t \nu_{st}\frac{z_{st}}{k_bT_{st}(m_s+m_t)}\left(m_t\frac{q_s}{n_s}-m_s\frac{q_t}{n_t}\right) \end{eqnarray*}$

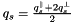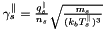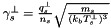We expand the heat flux with : $q_s = \frac{q_s^{\parallel} + 2q_s^{\perp}}{2}$ , and using the normalisation $\gamma_s^{\parallel} = \frac{q_s^{\parallel}}{n_s}\sqrt{\frac{m_s}{(k_bT_s^{\parallel})^3}}$ and $\gamma_s^{\perp} = \frac{q_s^{\perp}}{n_s}\sqrt{\frac{m_s}{(k_bT_s^{\perp})^3}}$ :

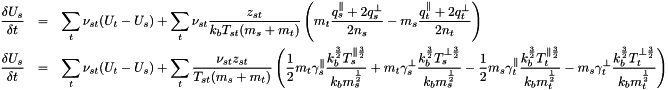
$\begin{eqnarray*} \frac{\delta U_s}{\delta t} &=& \sum_t \nu_{st}(U_t-U_s) + \sum_t \nu_{st}\frac{z_{st}}{k_bT_{st}(m_s+m_t)} \left(m_t\frac{q_s^{\parallel} + 2q_s^{\perp}}{2n_s}-m_s\frac{q_t^{\parallel} + 2q_t^{\perp}}{2n_t}\right)\\ \frac{\delta U_s}{\delta t} &=& \sum_t \nu_{st}(U_t-U_s) + \sum_t \frac{\nu_{st}z_{st}}{T_{st}(m_s+m_t)} \left( \frac{1}{2} m_t\gamma_s^{\parallel }\frac{k_b^{\frac{3}{2}}T_s^{\parallel \frac{3}{2}}}{k_b m_s^{\frac{1}{2}}} + m_t\gamma_s^{\perp }\frac{k_b^{\frac{3}{2}}T_s^{\perp \frac{3}{2}}}{k_b m_s^{\frac{1}{2}}} -\frac{1}{2} m_s\gamma_t^{\parallel }\frac{k_b^{\frac{3}{2}}T_t^{\parallel \frac{3}{2}}}{k_b m_t^{\frac{1}{2}}} - m_s\gamma_t^{\perp }\frac{k_b^{\frac{3}{2}}T_t^{\perp \frac{3}{2}}}{k_b m_t^{\frac{1}{2}}} \right) \end{eqnarray*}$

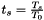$t_s = \frac{T_s}{T_0}$ is the normalised temperature.
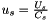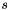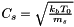$u_s = \frac{U_s}{C_s}$ is the normalised velocity for specie $s$ with $C_s = \sqrt{\frac{k_b T_0}{m_s}}$ .

$\begin{eqnarray*} \frac{\delta u_s}{\delta t} &=& \frac{1}{C_s}\frac{\delta U_s}{\delta t}\\ \frac{\delta u_s}{\delta t} &=& \frac{1}{C_s}\left[\sum_t \nu_{st}(u_t C_t - u_s C_s) + \sum_t \frac{\nu_{st}z_{st}}{t_{st}(m_s+m_t)} \left( \frac{1}{2} m_tC_s t_s^{\parallel \frac{3}{2}}\gamma_s^{\parallel } + m_tC_s t_s^{\perp \frac{3}{2}}\gamma_s^{\perp } -\frac{1}{2} m_sC_t t_t^{\parallel \frac{3}{2}}\gamma_t^{\parallel } - m_sC_t t_t^{\perp \frac{3}{2}}\gamma_t^{\perp } \right)\right]\\ \frac{\delta u_s}{\delta t} &=& \sum_t \nu_{st}(u_t \frac{C_t}{C_s} - u_s) + \sum_t \frac{\nu_{st}z_{st}}{t_{st}(m_s+m_t)} \left( \frac{1}{2} m_t t_s^{\parallel \frac{3}{2}}\gamma_s^{\parallel } + m_t t_s^{\perp \frac{3}{2}}\gamma_s^{\perp } -\frac{1}{2} m_s\frac{C_t}{C_s} t_t^{\parallel \frac{3}{2}}\gamma_t^{\parallel } - m_s\frac{C_t}{C_s} t_t^{\perp \frac{3}{2}}\gamma_t^{\perp } \right) \end{eqnarray*}$

Collision terms for ionic velocity
Collision terms for neutral velocity