Correction de la dispersion atmosphérique avec des prismes de Risley

Prismes de Risley de PISCO2.

a) Principe: correction par prismes de Risley

Pour un objet astronomique observé à une distance zénithale non nulle, l'atmosphère se comporte comme un prisme mince d'indice $n(\lambda)$ et produit un déplacement vertical de l'image, qui varie en fonction de la longueur d'onde $\lambda$. Pour de grandes distances zénithales, les étoiles paraissent ainsi plus hautes sur l'horizon qu'elles ne le sont véritablement. Cet angle de réfraction dépendant de la longueur d'onde, chaque image d'un objet observé près de l'horizon est en fait ``étirée'' en un petit spectre. Par exemple, si l'on considère une large bande passante, entre $H_\alpha$ et Ca$^{++}(K)$, on obtient une dispersion atmosphérique de l'ordre de 1 " pour une distance zénithale $z =40^\circ$ et 2 " pour $z =60^\circ$.

Cet effet est négligé dans la plupart des observations astronomiques, car la longueur de ce spectre dans le domaine visible est du même ordre que l'agitation des images causé par la turbulence atmosphérique. Par contre cet effet doit être impérativement corrigé lorsqu'on cherche à atteindre une résolution très inférieure à la seconde d'arc.

Pour notre instrument, la correction est faite grâce à un ensemble de deux jeux identiques de deux prismes. Chaque jeu est constitué par deux prismes d'indice et d'angle différents disposés tête-bèche. Ces deux prismes ont été calculés de façon à avoir une déviation moyenne nulle, avec une dispersion suffisante pour corriger les effets de l'atmosphère pour des observations jusqu'à une distance zénithale de 60$^\circ$.

Lors des observations, la distance zénithale est calculée ainsi que la dispersion atmosphérique qui en résulte. Les deux jeux sont alors orientés de façon à ce que leur dispersion totale soit égale en intensité à la dispersion atmosphérique, mais dans la direction opposée.

b) Dispersion atmosphérique

Pour notre problème, on peut considérer que la Terre est plate et l'atmosphère est modélisée par une couche plane homogène d'indice $n_{\hbox{\small\it air}}$. D'après la loi de Descartes:

$$%n' \sin z' = n_{\hbox{\small\it air}} \sin z\eqno{{\rm (1)}}$$

avec $n'$=1 (vide). L'angle $z$ entre la normale à la surface et l'objet correspond à ce que les astronomes appellent la distance zénithale. Dérivons cette relation par rapport à $\lambda$:

$$%0 = {dn_{\hbox{\small\it air}} \over d\lambda} \sin z+ {dz......er d\lambda} n_{\hbox{\small\it air}} \cos z\eqno{{\rm (2)}}$$

On obtient ainsi une expression de la dispersion atmosphérique (obtenue pour la première fois par Lambert en 1759):

$$%{dz \over d\lambda } =- {\tan z \over n_{\hbox{\small\it ......{dn_{\hbox{\small\it air}} \over d\lambda}\eqno{{\rm (3)}}$$

C'est donc la dépendance $n(\lambda)$ qui est essentielle pour notre problème. L'indice de l'atmosphère a été l'objet de nombreuses études et il existe un certain nombre de formules semi-empiriques. Nous utiliserons la formule de J.C Owens car elle est souvent citée dans la litérature astronomique.

J.C. Owens (1967) donne les expressions suivantes (formules n$^\circ$ 29 à 31 de son article):

$$\begin{eqnarray*}(n-1)\times10^{8} = &\displaystyle\left[ 2371.34 + { 683939.......^{-4}+ 0.08851 \lambda^{-6}\Bigr] D_w\qquad \hbox{\rm (4)}\cr\end{eqnarray*}$$

où $D_s$ et $D_w$ sont les facteurs de densité associés respectivement à l'air sec standard sans CO$_{2}$, et à la vapeur d'eau:

$$%D_s = { P_s \over T } \left[ 1+ P_s \left( 57.90\times10^...... T}+ { 0.25844 \over T^2 } \right) \right]\eqno{{\rm (5)}}$$

$$\begin{eqnarray*}D_w = { P_w \over T } &\displaystyle\left[ 1 + P_w \Bigl( 1 ......0^{4} \over T^3}\right)\right]\qquad \qquad \hbox{\rm (6)}\cr\end{eqnarray*}$$

Ici $P_s$ est la pression partielle de l'air sec standard supposé contenir 0.03% de CO$_2$ et $P_w$ est la pression partielle de la vapeur d'eau. Les unités sont les suivantes: pression en millibars, longeur d'onde en microns, température en degrés Kelvin.

Ces formules conduisent à des erreurs de l'ordre de $10^{-7}$--$10^{-8}$ sur l'indice de l'air dans les conditions proches des valeurs mesurées en laboratoire.

Simon (1966) a dérivé une expression plus précise qui tient compte de la rotondité de la Terre, et de la variation d'indice de l'air en fonction de l'altitude, mesurée par des fusées-sondes. Nous avons comparé numériquement ces formules et obtenu un très bon accord entre elles. Les formules de Simon n'étant valables que pour certaines conditions météorologiques, nous utiliserons de préférence les formules plus simples qui ne font intervenir qu'une valeur moyenne de l'indice de l'air.

b) Calcul de l'angle des prismes

Revenons donc à l'équation (3) pour estimer l'ordre de grandeur de la correction maximale à appliquer pour notre instrument dans des conditions ``standards'', avec un filtre V de 20 nm de bande passante, et une distance zénithale de 70$^\circ$.

En appliquant les formules de Owens (1967), avec $P$=720 mB, T=0$^\circ$C, un degré d'hygrométrie de 30%, $z$=70$^\circ$, $\lambda_1$=550 nm, et $\Delta \lambda$=20 nm, on obtient: $\Delta z$=0.17 " au niveau du foyer Cassegrain. Le tavelographe introduisant un grandissement de 250 fois (rapport entre les focales du télescope (50 m) et celle du collimateur (0.20 m)), il faut donc corriger une dispersion de $250 \Delta z$=0.20 mrad dans le faisceau parallèle, là où se trouvent les prismes de Risley.

Dans un cas très défavorable avec $P$=900 mB, T=0$^\circ$C, un degré d'hygrométrie de 100%, $z$=70$^\circ$, $\Delta z$=0.21 ", on obtient donc: $250 \Delta z$=0.25 mrad.

La correction maximale à appliquer est donc de 0.25 mrad.

La déviation d'un prisme mince d'angle $\beta$ est $\alpha = (n - 1) \beta$. Pour un jeu de deux prismes tête-bèche, d'indices $n_1$ et $n_2$ et d'angles $\beta_1$ et $\beta_2$, la déviation totale est donc $(n_1 - 1) \beta_1 - (n_2 - 1) \beta_2$. Nous voulons une deviation nulle pour $\lambda_0$=550 nm, donc nous avons une contrainte sur le rapport d'angles:

$$%\beta_2 / \beta_1 = (n_1(\lambda_0) - 1) / (n_2(\lambda_0) - 1)\eqno{{\rm (7)}}$$

Dans le cas de la combinaison F4-SK10, on a:
n$_{F4}$(550 nm)$=$1.62002, et n$_{SK10}$(550 nm)$=$1.62514. Donc

$$%\beta_2 / \beta_1 = 0.99182\eqno{{\rm (8)}}$$

Nous voulons que la dispersion de ce jeu de deux prismes puisse annuler la moitié (puisque nous disposons de deux jeux de deux prismes) de la dispersion atmosphérique $d z$ pour une distance zénithale de 70$^\circ$ et une bande passante de 20 nm, centrée sur $\lambda_1$=550 nm, ce qui se traduit par l'équation suivante:

$$%{ 1\over 2 }\times{d z \over d\lambda } =\beta_1 \times{ ......_2 \times{ d n_2 \over d\lambda }(\lambda_1)\eqno{{\rm (9)}}$$

Substituons:

$$%\beta_1 = { \Delta z / 2 \over\Delta n_1 - \Delta n_2 \ti......lambda_1) - 1 \over n_2(\lambda_1) - 1 }}}\eqno{{\rm (10)}}$$

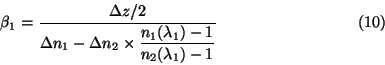
où $\Delta$ est la variation de la quantité concernée entre $\lambda_1 - 10$ nm et $\lambda_1 + 10$ nm.

Dans le cas de la combinaison de deux matériaux optiques ``standards'' du F4 et du SK10, on a: $\Delta n_{F4} =2.075 \times 10^{-3}$, $\Delta n_{SK10} =1.372 \times 10^{-3}$. Pour pouvoir corriger une dispersion atmosphérique de 0.25 mrad, il vient $\beta_{F4}$ = 9.98$^\circ$.

On prendra en fait: $\beta_{F4}$ = 10.00$^\circ$, et en tenant compte de la contrainte de déviation nulle (éq. (8)): $\beta_{SK10}$ = 9.92$^\circ$. Nous avons fait tailler ces prismes à la société "SOPTEL" pour PISCO en 1992.

Avec ces valeurs, pour des filtres ayant une bande passante de 100 nm, et balayant l'ensemble du spectre 400-1000 nm, la dispersion résiduelle maximale est inférieure à 0.015 ", même pour des conditions défavorables: P=1013 mB, T=0$^\circ$C, 100% d'hygrométrie, et $z$=65$^\circ$ (Cf description technique de PISCO ).

Pour PISCO2, installé sur le grande lunette de Nice (voir page web de PISCO2 ), le calcul précédent a conduit aux mêmes valeurs pour les angles des prismes que ceux de PISCO. Les prismes de PISCO2 ont étés réalisés par la société "Optique J. Fichou et Tofico" en 2012.

Une version plus complète (extraite de la thèse d'habilitation de Jean-Louis Prieur) est disponible dans le fichier risley.pdf)

Bibliographie:

Owens, J.C., 1967, Optical refractive index of air: dependence on pressure, temperature and composition, Applied Optics, Vol. 6, 1, 51-59.

Simon, G.W., 1966, A practical solution of the atmospheric dispersion problem, Astronomical Journal, 71, 190.