Les éléments principaux de notre instrument sont une lentille utilisant le principe de diffraction de Laue et un détecteur de taille réduite en Ge sur lequel est focalisé le rayonnement gamma. Ce type de télescope permet de surmonter l'impasse dans laquelle se trouve l'astronomie gamma actuelle, provenant principalement du fait que la surface du détecteur et la surface collectrice des photons ne font qu'une [voir les instruments de l'astrophysique nucléaire]. Dès lors, augmenter la surface collectrice (au prix d'un accroissement du poids, de l'encombrement et du prix du système...) engendre une augmentation du bruit de fond nuisible ce qui, en retour, limite fortement le gain en sensibilité.
 
 

Diffraction de Laue

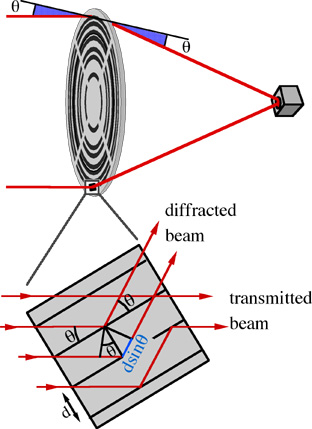Une onde plane monochromatique, tombe sur un cristal constitué d'une seule sorte d'atomes, tous disposés aux noeuds d'un réseau simple. Lorsque l'onde traverse le cristal, elle interagit avec les nuages électroniques des atomes répartis régulièrement. Les ondes elemenaires emises par les atomes interferent de façon constructive dans des directions données par la relation de Bragg                                 2 d sin(q) = nl ou d est la distance entre les plans cristallins, q l'angle de Bragg, l la longueur d'onde du photon et n est l'ordre de diffraction. Après son passage dans le cristal, un photon continue donc, avec une certaine probabilité, son chemin selon une nouvelle direction. Il est possible de profiter de la diffraction pour focaliser les photons en plaçant les cristaux sur des anneaux concentriques. A partir d'une grande surface collectrice, où sont disposés les cristaux les photons gamma sont focalisés sur une surface plus petite où l'on place le détecteur. 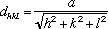Car le signal augmente sans accroître le bruit de fond, la sensibilité de ce type d'instrument La distance entre deux plans consécutifs [hkl] vaut où a est le paramètre de la maille. On remarque que pour le premier ordre (n=1) on doit respecter 2d * l à cause de la fonction sinus.Notons immediatement que les angles de Bragg seront très petits dans le cas des rayons gamma. Par exemple pour le plan [111] du Germanium on a, à 511 keV: l = 0.02478 Å, avec a = 5.657 Å,  d111 = 3.266 Å             =>             q111 = 0.217°

Il existe deux disposition géométriques pour la diffraction: celle de Bragg et celle de Laue. Dans le cas de Bragg la diffraction se produit à la surface du matériau ce qui diffère du modèle de Laue, où la diffraction se produit dans le volume du cristal et les rayons incidents arrivent sur la surface perpendiculaire aux plans cristallins. On remarque que la longueur de diffraction est moindre (dans le cas ci-dessus pour 4° d'incidence on a 14 et 1cm) ce qui implique moins d'épaisseur des cristaux pour avoir le même faisceau diffracté, et c'est pour cela que dans le cas de la lentille gamma on utilise la diffraction de Laue.
 

les cristaux de diffraction et les caractéristiques du télescope

Les caractéristiques du télescope et ses performances sont pour la plupart déterminées par les cristaux utilisés. La bande passante d'énergie et le champ-de-vue du télescope sont corrélés et déterminés par la mosaïcité des cristaux. Ceci est dû à la relation de Bragg  2 d sin(q) = nl. En différentiant cette relation on obtient: DE/E = Dq/q, où DE est la bande passante de la lentille et Dq la mesure de la mosaïcité du cristal. Ainsi, la mosaïcité définit Dq et par suite DE. D'autre part, l'intensité de diffraction est un fonction de q-Dq , la différence entre l'angle incidence et l'angle de Bragg. Pour une source étendue avec une dispersion angulaire, la bande d'énergie focalisée par la lentille est une convolution de cette fonction d'intensité avec le flux de la source.

Pour des observations astrophysique, Dq ne doit pas être plus petit que quelques secondes d'arc pour deux raisons: le pointage d'une nacelle ballon ou d'une expérience embarquée sur satellite serait problématique et, en outre, on diminue la sensibilité si la bande passante en l'énergie pour une source gamma est trop étroite. D'autre part, une mosaïcité qui excède une minute d'arc va limiter le pouvoir de localisation du télescope, une cartographie de l'intensité des sources étendues de la seconde d'arc à la minute d'arc n'est plus possible. De plus, l'efficacité de diffraction décroît avec une augmentation de mosaïcité. Pour des raisons de pointage / pouvoir de localisation, le choix optimal de mosaïcité ne coïncide pas nécessairement avec la meilleure sensibilité.