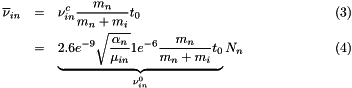
Collision frequency in the laboratory system VS collision frequency in the center of mass coordinate system:

$\nu_{12} = \nu^c_{12}\frac{m_2}{m_1+m_2}$

From ..., in the center of mass coordinate system:

$\nu^c_{ij} = A \frac{\left(z_i z_j\right)^2}{\mu_{ij}} N_j T_{i}^{-\frac{3}{2}}\\$

with $[\nu^c_{ij}]=s^{-1}$ , $[N_j]=m^{-3}$ , $[\mu_{in}]=amu$ .

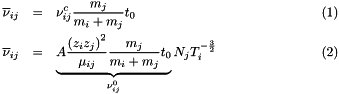
$\begin{eqnarray} \overline{\nu}_{ij} &=& \nu^c_{ij} \frac{m_j}{m_i+m_j} t_0\\ \overline{\nu}_{ij} &=& \underbrace{A \frac{\left(z_i z_j\right)^2}{\mu_{ij}} \frac{m_j}{m_i+m_j} t_0}_{\nu_{ij}^0} N_j T_{i}^{-\frac{3}{2}} \end{eqnarray}$

From Banks et Kockarts (A, p218), in the center of mass coordinate system:

$\nu^c_{in} = 2.6e^{-9}\sqrt{\frac{\alpha_n}{\mu_{in}}}N_n1e^{-6}$

with $[\nu^c_{in}]=s^{-1}$ , $[N_n]=m^{-3}$ , $[\alpha]=10^{-24}cm^3$ , $[\mu_{in}]=amu$ .

$\begin{eqnarray} \overline{\nu}_{in} &=& \nu^c_{in} \frac{m_n}{m_n+m_i} t_0\\ &=& \underbrace{2.6e^{-9}\sqrt{\frac{\alpha_n}{\mu_{in}}}1e^{-6}\frac{m_n}{m_n+m_i}t_0}_{\nu_{in}^0}N_n \end{eqnarray}$

From Schunk et Nagy 1980 p822, in the center of mass coordinate system:

$\nu^c_{en} = A^{res}_{en}N_n 1e^{-6}f(T_e)$

with $[\nu^c_{en}]=s^{-1}$ , $[N_n]=m^{-3}$ , $[T_e]=K$ .

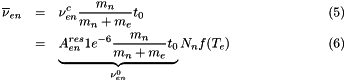
$\begin{eqnarray} \overline{\nu}_{en} &=& \nu^c_{en} \frac{m_n}{m_n+m_e} t_0\\ &=& \underbrace{A^{res}_{en}1e^{-6} \frac{m_n}{m_n+m_e} t_0}_{\nu_{en}^0} N_n f(T_e) \end{eqnarray}$

From Schunk et Nagy 1980 p822, in the center of mass coordinate system:

$\nu^c_{in} = A^{res}_{in}N_n 1e^{-6}T_r^{\frac{1}{2}}\left(1-B_{in}log_{10}T_r\right)^2$

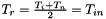with $[\nu^c_{in}]=s^{-1}$ , $[N_n]=m^{-3}$ , $[T_e]=K$ and $T_r = \frac{T_i + T_n}{2} = T_{in}$ in case of ion-neutral parent.

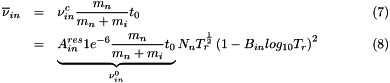
$\begin{eqnarray} \overline{\nu}_{in} &=& \nu^c_{in} \frac{m_n}{m_n+m_i} t_0\\ &=& \underbrace{A^{res}_{in}1e^{-6} \frac{m_n}{m_n+m_i} t_0}_{\nu_{in}^0} N_n T_r^{\frac{1}{2}}\left(1-B_{in}log_{10}T_r\right)^2 \end{eqnarray}$

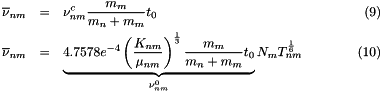
From ..., in the center of mass coordinate system:

$\nu^c_{nm} = 4.7578e^{-4} \left(\frac{K_{nm}}{\mu_{nm}}\right)^{\frac{1}{3}} N_m T_{nm}^{\frac{1}{6}}$

with $[\nu^c_{nm}]=s^{-1}$ , $[N_m]=m^{-3}$ , $[\mu_{nm}]=amu$ .

$\begin{eqnarray} \overline{\nu}_{nm} &=& \nu^c_{nm} \frac{m_m}{m_n+m_m} t_0\\ \overline{\nu}_{nm} &=& \underbrace{4.7578e^{-4} \left(\frac{K_{nm}}{\mu_{nm}}\right)^{\frac{1}{3}} \frac{m_m}{m_n+m_m} t_0}_{\nu_{nm}^0} N_m T_{nm}^{\frac{1}{6}} \end{eqnarray}$

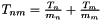with $T_ {nm} = \frac{T_n}{m_n} + \frac{T_m}{m_m}$ .