Théorie de l’information    PAEL5

Corrigé 2.1 :  Hors du temps

1)  Chaque pixel peut prendre 2²⁴ valeurs (états) possibles. Comme on suppose que les pixels sont indépendants les uns des autres, le nombre d’états possibles d’un système de 1000*1000 pixels est de

N =  (2²⁴ )^{1000 000} = 2 ^{24 000 000} = 10 ^{7 200 000}

2) durée de traitement d’une image : t = 10 ^{- 12} s
durée totale : T = t N  =  10 ^{7 200 000 - 12} s ;

ou T = 10 ^{7 200 000 - 30} fois l’âge actuel de l’univers :  on est carrément “hors du temps”.

3) avec une image 10*10 sur 1 bit par pixel : N’ = 2 ¹⁰⁰ = 10 ³⁰
durée totale T’ = t N’ = 10 ^{30 - 12} s = 10 ¹⁸ s = 31 milliards d’années, soit environ deux fois l’âge actuel de l’univers.

On peut estimer de la même façon la durée qu’il faudrait pour “craquer” par force brute une clé informatique codée sur 100 bits.

Corrigé 2.2 :  Mémoire ADN

Si l’on prend comme mesure de l’information G le nombre de bases, on a
 G = log₄ (N)

D’autre part, si l’on applique la formule
 G = k lb (N)

on trouve
k = log ₄ (N) /  log ₂ (N)

k = ln ₂ / ln ₄    =    0,5.

On retrouve ce résultat intuitivement car une base (ou codon) ADN peut prendre 4 valeurs, donc vaut 2 bits.

Réflexions ...
Qu’est-ce qui contient le plus d’information dans le corps hmain : le cerveau ou le code génétique ? (et ne me dites pas : “Ca dépend qui ! ” )

Corrigé 2.3 :   Entropie thermodynamique et entropie de Shannon.

H = S / (Kb ln 2)    car    lb x = ln x / ln 2
H = 1,046 10 ²³ S
Un Joule par Kelvin (unité d’entropie thermodynamique) correspond à 10 ²³ bits environ.

Réflexions ...
y a-t-il une raison physique pour que cette quantité soit commensurable avec le nombre d’Avogadro ?
Peut-on exprimer le nombre de bits par atome à une température donnée ? Quelle serait la relation avec les états d’énergie dans un atome ?
Parmi les mémoires suivantes, laquelle est la plus compacteen bits par kg :
- livre
- DVD
- chip RAM de 1 Gigabit
- synapse de neurone
- ADN
Comment évaluer la limite théorique à la capacité d’une mémoire ?

Corrigé 2.4 :   Additivité de l’ info de deux événements indépendants

Si l’on observe l’un des deux événements, on a :
I(x₁) = - lb P(x₁)   ou bien  I(x₂) = - lb P(x₂) .

Si l’on observe les deux événements, on a :
I(x₁, x₂) = - lb P(x₁, x₂) .

Comme les événements x1 et x2 sont indépendants,P(x₁, x₂) = P(x₁) P(x₂),   donc
I(x₁, x₂) = - lb P(x₁) - lb P(x₂) = I(x₁) +  I(x₂) .

Corrigé 3.1 :      Entropie d’une source à deux états de probabilités inégales.

 Si l’état “1” a un proba P1, alors l’état “2” a pour proba: P2 =  1 - P1.

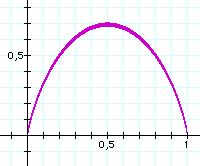
H(P1) = -P1 lb P1 - (1-P1) lb(1-P1)

H(P1) =  f(x) / ln 2    avec:

x = P1   et   f(x) = - [ x ln x  + (1-x) ln (1-x) ]

c’est une fonction symétrique par rapport à x = 1/2 car inchangée si l’on remplace x par 1-x.

f’(x) = - [ ln x + 1 - ln (1-x) + -1 ]  =  ln (1-x) - ln x
 

x	0	1/2	1
f(x)	0	1/ln2	0
f’ (x)	+inf	0	-inf

ccorrigé 3.2 :    Débit de fax.

1)   1,45  M bits. Pour transmettre cette quantité d’information en 10 s il faut un débit de 145 k bits s^{- 1} . C’est trop pour la ligne considérée.

2a)  h = -  0,01 lb 0,01 - 0,99 lb 0,99 = 0,081 bit

2b)  Pour toute la page H = 117 k bits. Pour transmettre cette quantité d’information en 10 s il faut un débit de : 11,7 k bits s^{- 1} . C’est possible avec un canal de débit  28,8 k  bits s^{- 1} à condition d’utiliser un codage proche de l’optimal.

Exercice 3.3 :   compression vidéo.

1) 256 niveaux, de 400 x 500 pixels => H = 8*400*500 = 1,6 M bit

2)  Coder non pas la brillance d’un pixel mais la différence de brillance entre deux pixels consécutifs.

P(0) = 1/2 ; P(1) = 1/4 ; P(-1) = 1/4 ;
Entropie : 1/2+1/2+1/2 = 1,5  bits par pixel au lieu de 8 sans compression.

3) Pour améliorer encore la compression on peut combiner le codage précédent avec la différence entre un pixel et son homologue dans l’image suivante. P(0) sera encore augmenté, d’où une réduction de H.

Exercice 3.4 :   l’esprit  frappeur...

1) Nombre moyen de bits par symbole avec le code utilisé :
(2+3+...+27)/26 = 29/2 = 14,5

2) Entropie de la source : lb (27) = 4,75

3) Exemple de codage meilleur
binaire sur 5 bits: A->0001 ; B->0010 ; C->0011 ; D->0100 ; E->0101 etc.
On a alors 5 bits par symbole, ce qui se rapproche de l’entropie de la source.

4) gaffe au chat noir, il griffe *@!!

Corrigé 4.1 :   La distance de Kullback-Lieber est positive  " Qi  et  Pi .

Démonstration :

Dans la suite,
le caractere : S   devrait apparaitre comme le caractere grec "Sigma"  ou "Somme de".
le caractere  : ?  devrait apparaitre comme "inférieur ou égal"
le caractere : *  devrait apparaitre comme "supérieur ou égal"

Soit Ui  =  Qi  - Pi ,  la différence entre les deux probas.

 S Pi lb Qi  =  S Pi lb (Pi + Ui )

 S Pi lb Qi  =  S Pi lb [Pi (1 + Ui /Pi)]

 S Pi lb Qi  =   S Pi [ lb Pi + lb (1 + Ui /Pi)]

 S Pi lb Qi  =  S Pi lb Pi +S Pi lb (1 + Ui /Pi)]

or   lb (1+x) = ln (1+x)  /  ln 2

et ln (1+x) ? x   pour tout x   =>  lb (1+x) ?  x  /  ln 2   pour tout x.

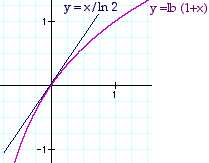
 =>  Pi  lb (1 + Ui /Pi)  ?  Pi Ui /Pi  ln 2

=>  S Pi  lb (1 + Ui /Pi)  ?  (1/ ln 2) S Ui

 or  d’après le définition de Ui  on voit que  S Ui  = 0.

=>  S Pi  lb (1 + Ui /Pi)  ? 0 .

et en revenant à l’expression du départ cela implique :

 Somme Pi lb Qi  ? S Pi lb Pi ,

=>  Somme Pi ( lb Qi  -  lb Pi) ? 0 ,

=>  K = + Somme Pi lb (Pi /Qi )  * 0 .

orrigé 5.1 :    Redondance du langage.

Non, car le canal est bien discret, mais non sans mémoire : La probabilité d’une lettre dépend des précédentes, par exemple la probabilité d’un “u” après un “q” est bien plus élevée que celle d’un “z” après un “q”.

orrigé 5.2 :

On a donc :
H(X) = 0,971   ;   H(Y) = 1

M (X,Y)  =  M (X ) M (Y|X)

H (X, Y)  = - S_e S_r P(x_e , y_r ) lb [  P(x_e , y_r ) ]

H (X, Y)  = 0,526 + 0,292 + 0,445 + 0,526 = 1,788

H (X|Y) = H (X, Y) - H(Y) = 0,788

I(X,Y) = H(X)  -  H (X|Y) = 0,971 - 0,788 = 0,183