Heure des cadrans solaires
Nous allons essayer de répondre à quelques questions concernant les cadrans solaires. Nous n'avons pas la prétention de concurrencer les excellents sites qui existent et qui expliquent en détails comment réaliser des cadrans solaires. En fait, nous voudrions seulement répondre à cette question: quelle heure indiquent les cadrans solaires et comment relier cette "heure solaire" à l'heure donnée par les montres?
---------------------------------------------------------------------------------
Question 1: quelle heure doit indiquer un cadran solaire, par exemple à Toulouse le 20 nov. 2006 à 11H (temps légal en France)? quel est le temps universel correspondant ?
Réponse: un quadrant solaire indique le temps solaire local (TLoc) du lieu où il se trouve.
Ainsi donc, il doit
indiquer midi lorsque le Soleil passe au méridien
(c'est-à-dire
lorsqu'il culmine en plein Sud).
Cette réponse ne vous semble
peut-être pas très claire. Pour aller plus loin, il est
nécessaire de rappeler quelques définitions:
Temps solaire local (TLoc): c'est l'angle horaire du
Soleil (angle entre le Soleil et le méridien du lieu), plus 12
heures.Méridien local: plan Sud-Nord passant par l'observateur. On peut le repérer avec une boussole (avec les corrections relatives à la position du pôle magnétique, indiquées sur les cartes IGN par exemple) ou la nuit avec l'étoile polaire (et les corrections indiquées sur des cartes célestes).
Temps Universel (TU): temps utilisé comme référence dans le monde entier. Il correspond approximativement au temps solaire moyen local sur le méridien de Greenwich.
Temps légal en France (TL): il est égal à TU+2H en été, et à TU+1H en hiver.
Soit: TL = TU + m avec m= 2H en été et m=1H en hiver.
Longitude (L): angle entre le méridien du lieu et le méridien de Greenwich. Cet angle est positif vers l'ouest et négatif vers l'est (pour Toulouse, L = - 1 degré 26' 34").
-------------------------------------------------------------------------------------
Question2: comment obtenir TLoc, le temps solaire local à Toulouse, à partir de sa montre, qui indique le temps légal (TL)?
1. Première approximation:
TLoc = TU ou TLoc = TL - m avec m= 2H en été et m=1H en hiver (formule précise à +/- 22 minutes)
Donc, pour obtenir TLoc à partir de l'heure de sa montre, il faut enlever 2 heures en été, 1 heure en hiver.
2. Deuxième approximation:
TLoc = TU - L ou TLoc = TL - m - L avec m= 2H en été et m=1H en hiver (formule précise à +/- 16 minutes)
Pour Toulouse, L = - 1 degré 26' 34", soit -5.77 minutes de temps (rappel: 1 degré = 24 * 60 / 360 minutes de temps)
En hiver: pour obtenir TLoc à partir de l'heure légale, il faut enlever 2 heures et rajouter 5.77 minutes. En été: il faut enlever 1 heure et rajouter 5.77 minutes.
3. Formule exacte:
TLoc = TL - m - E - L où E est "l'équation du temps" (voir détails ci-dessous).
Pour améliorer la précision, on a introduit le terme correctif E ("équation du temps"), qui varie au cours de l'année entre +14 et - 16 minutes. Ce terme est assez compliqué à calculer (voir détails ci-dessous). On peut trouver des tables qui donnent E en fonction du jour de l'année dans des livres d'astronomie ou sur des sites internet (voir plus loin).
----------------------------------------------------------------------------------------------------
Question 3: Comment calculer le terme E (équation du temps)?
1. Origine de ce terme de correction
L'écart E qui intervient dans la formule "exacte" est la somme de deux termes: E = C + R, que nous allons détailler ici.
1) Le premier terme C est appelé "équation du centre".
Il traduit le fait que le mouvement de la Terre autour du soleil n'est pas uniforme, car l'excentricité de l'orbite terrestre n'est pas nulle (e=0.01671). La Terre tourne plus vite autour du Soleil lorsqu'elle est plus près du Soleil (le périhélie terrestre a lieu le 3 janvier) et ralentit lorsqu'elle s'éloigne du Soleil.
Remarque: bien sûr, la rotation de la Terre sur elle-même n'est pas affectée par ce phénomène!
2) Le deuxième terme R est la "réduction à l'équateur".
L'équateur terrestre (sur lequel est défini l'angle horaire) ne coïncide pas avec l'écliptique (= plan orbital annuel terrestre). L'angle dièdre entre ces deux plans est epsilon = 23 deg 27'. L'écart est donné par:
R = alpha - lambda
où alpha est l'ascension droite du Soleil (repérée sur l'équateur à partir de gamma, le point vernal) et lambda, la longitude écliptique du Soleil (mesurée sur l'écliptique à partir du point gamma).
Remarque: le point gamma est le noeud ascendant du Soleil, qui correspond à la position apparente du Soleil sur le ciel, lors de l'équinoxe du printemps, vers le 21 mars. Il correspond aussi à l'une des deux intersections du plan de l'écliptique avec le plan équatorial terrestre.
2. Formules de calcul
On a donc: E = C + R. Explicitons ces deux termes.
Introduisons la variable tau, qui mesure le mouvement moyen apparent du Soleil à partir du périhélie:
tau = 24 heures * N / 365.2422,
où N est la durée exprimée en jours écoulés depuis le passage au périhélie (le 3 janvier). On a alors:
C = 2 e sin tau + 5/4 e² sin 2 * tau
ou C = 459.6 sin tau + 4.8 sin² tau (en secondes)
La longitude écliptique moyenne du soleil est lbda = tau - 77.8 degrés (afin d'obtenir lbda = 0, lors de l'équinoxe du printemps).
R = - tan² (epsilon/2) * sin (2 lbda) + 1/2 tan^4 (epsilon/2) sin(4 lbda)
ou R = - 591.85 sin( 2 lbda) + 12.73 sin (4 lbda) (en secondes)
Avec ces formules, on obtient E en fonction du jour de l'année. Vers le 11 février, on a E = +14 minutes: le Soleil culmine au méridien 14 minutes plus tard qu'en moyenne, tandis qu'il est en avance vers le 3 novembre, avec E = - 16 minutes.
Voici un exemple de courbe calculée par le Bureau des Longitudes pour les éphémérides de 1987 de la Société Astronomique de France:
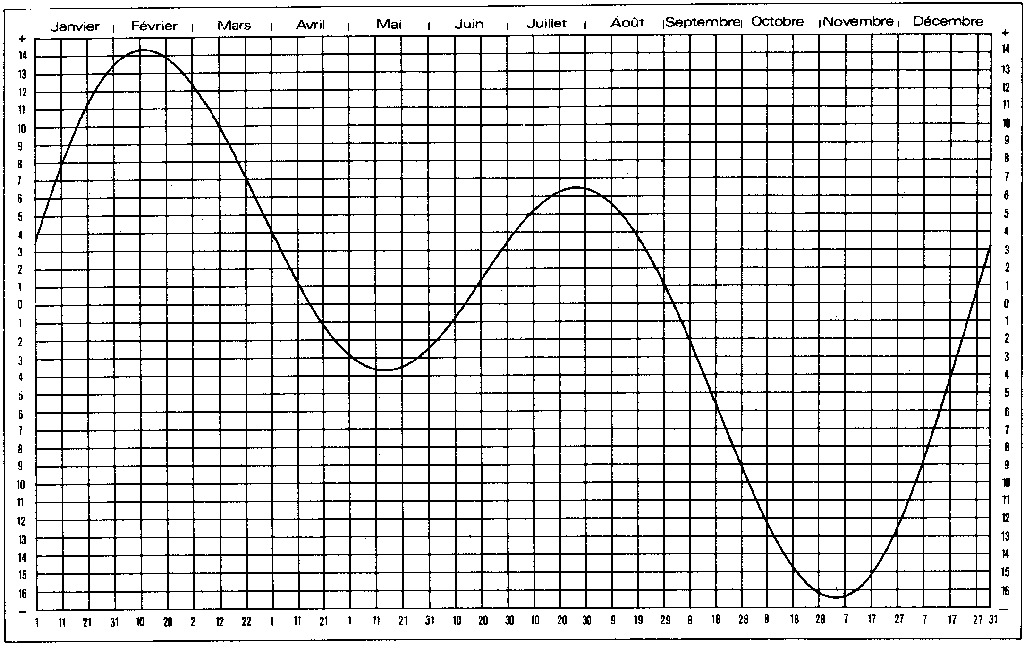
L'Association des Astronomes Amateurs d'Auvergne propose sur son site expliquant comment faire un cadran solaire horizontal de télécharger une version de cette courbe en 300 ppp.
Pour rédiger la partie ayant trait à l'équation du temps, j'ai utilisé la page http://obswww.unige.ch/Questions_Reponses/R23.html de Bernard Nicolet de l'Observatoire de Genève.